
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�������y=x2+![]() ��y���ཻ�ڵ�A����B���O���ڵ�A�Գ�
��y���ཻ�ڵ�A����B���O���ڵ�A�Գ�

��1����գ���B�������� ��
��2������B��ֱ��y=kx+b������k��0����x���ཻ�ڵ�C������C��ֱ��lƽ����y�ᣬP��ֱ��l��һ�㣬��PB=PC�����߶�PB�ij����ú�k��ʽ�ӱ�ʾ�������жϵ�P�Ƿ����������ϣ�˵�����ɣ�
��3���ڣ�2���������£�����C����ֱ��BP�ĶԳƵ�C��ǡ�����ڸ������ߵĶԳ����ϣ����ʱ��P�����꣮
���𰸡���1����0��![]() ������2����P����������,���������������3��P������Ϊ��
������2����P����������,���������������3��P��������![]() ��1����
��1����
�������������������1���������߽���ʽ����õ�A�����꣬�����öԳƿ����B�����ꣻ��2��������k��ʾ��C�����꣬��B��BD��l�ڵ�D��������֪P����x���Ϸ�����P��������Ϊy���ɱ�ʾ��PD��PB�ij�����Rt��PBD�У����ù��ɶ��������y��������PB�ij�����ʱ�ɵó�P�����꣬���������߽���ʽ���ж�P�����������ϣ���3������ƽ���ߺ���ԳƵ����ʿɵõ���OBC=��CBP=��C��BP=60����������OC�ij������������߽���ʽ�����P�����꣮
�����������1����������y=x2+![]() ��y���ཻ�ڵ�A��
��y���ཻ�ڵ�A��
��A��0��![]() ����
����
����B���O���ڵ�A�Գƣ�
��BA=OA=![]() ��
��
��OB=![]() ����B��������0��
����B��������0��![]() ����
����
�ʴ�Ϊ����0��![]() ����
����
��2����B��������0��![]() ����
����
��ֱ�߽���ʽΪy=kx+![]() ����y=0�ɵ�kx+
����y=0�ɵ�kx+![]() =0�����x=��
=0�����x=��![]() ��
��
��OC=��![]() ��
��
��PB=PC��
����Pֻ����x���Ϸ���
��ͼ1����B��BD��l�ڵ�D����PB=PC=m��
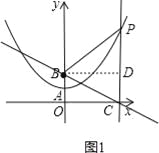
��BD=OC=��![]() ��CD=OB=
��CD=OB=![]() ��
��
��PD=PC��CD=m��![]() ��
��
��Rt��PBD�У��ɹ��ɶ����ɵ�PB2=PD2+BD2��
��m2=��m��![]() ��2+����
��2+����![]() ��2�����m=
��2�����m=![]() +
+![]() ��
��
��PB=![]() +
+![]() ��
��
��P����������![]() ��
��![]() +
+![]() ����
����
��x=��![]() ʱ�����������߽���ʽ�ɵ�y=
ʱ�����������߽���ʽ�ɵ�y=![]() +
+![]() ��
��
����P���������ϣ�
��3����ͼ2������CC����
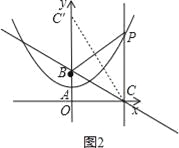
��l��y�ᣬ
���OBC=��PCB��
��PB=PC��
���PCB=��PBC��
���PBC=��OBC��
��C��C������BP�Գƣ���C���������ߵĶԳ����ϣ�����y���ϣ�
���PBC=��PBC����
���OBC=��CBP=��C��BP=60����
��Rt��OBC��OB=![]() ����BC=1
����BC=1
��OC=![]() ����P��ĺ�����Ϊ
����P��ĺ�����Ϊ![]() �����������߽���ʽ�ɵ�y=��
�����������߽���ʽ�ɵ�y=��![]() ��2+
��2+![]() =1��
=1��
��P��������![]() ��1����
��1����


 ��Ȥ����¹�֪��ϵ�д�
��Ȥ����¹�֪��ϵ�д� Ӣ��СӢ������Ĭдϵ�д�
Ӣ��СӢ������Ĭдϵ�д� �����ҵ���������ͯ������ϵ�д�
�����ҵ���������ͯ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾��֯Ա���������![]() �ס�������������Ϊ����������Ĺ˿ͣ��ֱ��Ƴ������ε������Żݰ취
�ס�������������Ϊ����������Ĺ˿ͣ��ֱ��Ƴ������ε������Żݰ취![]() ����������Żݰ취�ǣ���4��ȫƱ�������˰�ԭ�۵������շѣ�����������Żݰ취�ǣ�һ�ɰ�ԭ�۵������շ�
����������Żݰ취�ǣ���4��ȫƱ�������˰�ԭ�۵������շѣ�����������Żݰ취�ǣ�һ�ɰ�ԭ�۵������շ�![]() ��֪�������������ԭ�۾�ΪaԪ���������й����еĸ��ַ���������ͬ
��֪�������������ԭ�۾�ΪaԪ���������й����еĸ��ַ���������ͬ![]() ������Ǹù�˾�ĸ����ˣ����ѡ���ļ�������.
������Ǹù�˾�ĸ����ˣ����ѡ���ļ�������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD����AB��DC����ABC��90������A��45����AB��30��BC��x������15<x<30.����D��DE��AB�ڵ�E������ADE��ֱ��DE�۵���ʹ��A���ڵ�F����DF��BC�ڵ�G.

(1)�ú�x�Ĵ���ʽ��ʾBF�ij���
(2)���ı���DEBG�����ΪS����S����x�ĺ�������ʽ��
(3)��xΪ��ֵʱ��S�����ֵ�������������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������κ���y��x2��ͼ������ƽ��m��m��0������λ������ƽ��2����λ����ƽ���Ժ�Ķ��κ����Ľ���ʽΪ��������
A.y����x+2��2��mB.y����x+2��2+mC.y����x+m��2+2D.y����x��2��2+m
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ���˽���꼶��ѧ����ĩ������ѧ�ɼ����Ӿ��꼶ѧ���������ȡ�˲���ѧ�����е��飬��������ȡ��ѧ����ѧ�ɼ����ɼ���Ϊ��������ΪA��B��C��D��E����ȼ���A��50.5��60.5��B��60.5��70.5��C��70.5��80.5��D��80.5��90.5��E��90.5��100.5������������ͼ��ʾ��Ƶ���ֲ�ֱ��ͼ������ͳ��ͼ���������ͳ��ͼ�ṩ����Ϣ����������⣺ 
��1����γ������鹲��ȡ�˶�����ѧ����
��2�����Ƶ���ֲ�ֱ��ͼ����������
��3�������ĩ������ѧ�ɼ�����λ�������ĸ��ȼ��ڣ�
��4����У���꼶��800��ѧ�������涨80�����ϣ�����80�֣�Ϊ���ã��Թ��ƾ��꼶�ж�����ѧ������ѧ�ɼ�Ϊ���ã�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����и�ʽһ���������� �� ��
A.a2��0
B.a2=����a��2
C.a2=��a2
D.a3=��a3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ҹ��Ŵ��ķ��ݽ����У���������Ҫ����ɲ��֣����и߶ȵ�������ֵ�����д�����ͼ���У������ĶԳ�ͼ�ε�������Գ�ͼ�ε��ǣ� ��
A.
B.
C.
D.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com