
【题目】(6分)如图①所示,将直尺摆放在三角板ABC上,使直尺与三角板的边分别交于点D,E,F,G,量得∠CGD=42°。
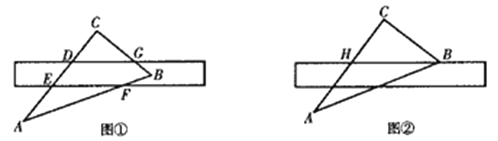
(1)求∠CEF的度数;
(2)将直尺向下平移,使直尺的边缘通过三角板的顶点B,交AC边于点H,如图②所示.点H,B在直尺上的读数分别为4,13.4,求BC的长(结果保留两位小数).
(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线y=x+1与x轴、y轴分别交于点A,B,抛物线y=ax2+bx-3a(a>0)经过点A将点B向右平移5个单位长度,得到点C.
(1)求点C的坐标;
(2)求抛物线的对称轴;
(3)若抛物线与线段BC恰有一个公共点,结合函数图象,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=﹣x2+bx+c(b,c为常数)的图象经过点A(3,1),点C(0,4),顶点为点M,过点A作AB∥x轴,交y轴于点D,交该二次函数图象于点B,连结BC.
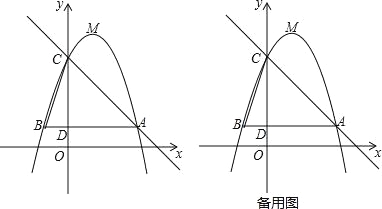
(1)求该二次函数的解析式及点M的坐标;
(2)若将该二次函数图象向下平移m(m>0)个单位,使平移后得到的二次函数图象的顶点落在△ABC的内部(不包括△ABC的边界),求m的取值范围;
(3)点P是直线AC上的动点,若点P,点C,点M所构成的三角形与△BCD相似,请直接写出所有点P的坐标(直接写出结果,不必写解答过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中装有红、黄两种颜色的球共20个,每个球除颜色外完全相同.某学习兴趣小组做摸球实验,将球搅匀后从中随机摸出1个球,记下颜色后再放回袋中,不断重复.下表是活动进行中的部分统计数据.
摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到红球的次数m | 59 | 96 | 118 | 290 | 480 | 601 |
摸到红球的频率 | 0.59 | 0.58 | 0.60 | 0.601 |
(1)完成上表;
(2)“摸到红球”的概率的估计值 (精确到0.1)
(3)试估算袋子中红球的个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B、C重合),以AD为直角边在AD右侧作等腰直角三角形ADE,且∠DAE=90°,连接CE.

(1)如图①,当点D在线段BC上时:
①BC与CE的位置关系为 ;
②BC、CD、CE之间的数量关系为 .
(2)如图②,当点D在线段CB的延长线上时,结论①,②是否仍然成立?若不成立,请你写出正确结论,并给予证明.
(3)如图③,当点D在线段BC的延长线上时,BC、CD、CE之间的数量关系为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC=8,BD=6,点E,F分别是边AB,BC的中点,点P在AC上运动,在运动过程中,存在PE+PF的最小值,则这个最小值是( )

A. 3 B. 4 C. 5 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了解本地七年级学生寒假期间参加社会实践活动情况,随机抽查了部分七年级学生寒假参加社会实践活动的天数(“A﹣﹣﹣不超过5天”、“B﹣﹣﹣6天”、“C﹣﹣﹣7天”、“D﹣﹣﹣8天”、“E﹣﹣﹣9天及以上”),并将得到的数据绘制成如下两幅不完整的统计图.
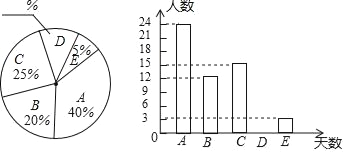
请根据以上的信息,回答下列问题:
(1)补全扇形统计图和条形统计图;
(2)所抽查学生参加社会实践活动天数的众数是 (选填:A、B、C、D、E);
(3)若该市七年级约有2000名学生,请你估计参加社会实践“活动天数不少于7天”的学生大约有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com