
ЁОЬтФПЁПШчЭМЃЌвбжЊЖўДЮКЏЪ§y=Љx2+bx+cЃЈbЃЌcЮЊГЃЪ§ЃЉЕФЭМЯѓОЙ§ЕуAЃЈ3ЃЌ1ЃЉЃЌЕуCЃЈ0ЃЌ4ЃЉЃЌЖЅЕуЮЊЕуMЃЌЙ§ЕуAзїABЁЮxжсЃЌНЛyжсгкЕуDЃЌНЛИУЖўДЮКЏЪ§ЭМЯѓгкЕуBЃЌСЌНсBCЃЎ
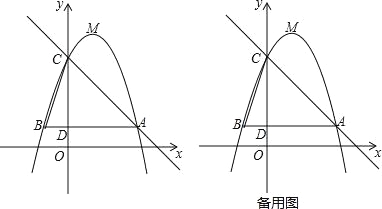
ЃЈ1ЃЉЧѓИУЖўДЮКЏЪ§ЕФНтЮіЪНМАЕуMЕФзјБъЃЛ
ЃЈ2ЃЉШєНЋИУЖўДЮКЏЪ§ЭМЯѓЯђЯТЦНвЦmЃЈmЃО0ЃЉИіЕЅЮЛЃЌЪЙЦНвЦКѓЕУЕНЕФЖўДЮКЏЪ§ЭМЯѓЕФЖЅЕуТфдкЁїABCЕФФкВПЃЈВЛАќРЈЁїABCЕФБпНчЃЉЃЌЧѓmЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉЕуPЪЧжБЯпACЩЯЕФЖЏЕуЃЌШєЕуPЃЌЕуCЃЌЕуMЫљЙЙГЩЕФШ§НЧаЮгыЁїBCDЯрЫЦЃЌЧыжБНгаДГіЫљгаЕуPЕФзјБъЃЈжБНгаДГіНсЙћЃЌВЛБиаДНтД№Й§ГЬЃЉЃЎ
ЁОД№АИЁПЃЈ1ЃЉy=Љx2+2x+4ЃЛMЃЈ1,5ЃЉЃЛЃЈ2ЃЉ2ЃМmЃМ4ЃЛЃЈ3ЃЉP1ЃЈ![]() ЃЉЃЌP2ЃЈ
ЃЉЃЌP2ЃЈ![]() ЃЉЃЌP3ЃЈ3ЃЌ1ЃЉЃЌP4ЃЈЉ3ЃЌ7ЃЉЃЎ
ЃЉЃЌP3ЃЈ3ЃЌ1ЃЉЃЌP4ЃЈЉ3ЃЌ7ЃЉЃЎ
ЁОНтЮіЁП
ЪдЬтЗжЮіЃКЃЈ1ЃЉНЋЕуAЁЂЕуCЕФзјБъДњШыКЏЪ§НтЮіЪНЃЌМДПЩЧѓГіbЁЂcЕФжЕЃЌЭЈЙ§ХфЗНЗЈЕУЕНЕуMЕФзјБъЃЛЃЈ2ЃЉЕуMЪЧбизХЖдГЦжсжБЯпx=1ЯђЯТЦНвЦЕФЃЌПЩЯШЧѓГіжБЯпACЕФНтЮіЪНЃЌНЋx=1ДњШыЧѓГіЕуMдкЯђЯТЦНвЦЪБгыACЁЂABЯрНЛЪБyЕФжЕЃЌМДПЩЕУЕНmЕФШЁжЕЗЖЮЇЃЛЃЈ3ЃЉгЩЬтвтЗжЮіПЩЕУЁЯMCP=90ЁуЃЌдђШєЁїPCMгыЁїBCDЯрЫЦЃЌдђвЊНјааЗжРрЬжТлЃЌЗжГЩЁїPCMЁзЁїBDCЛђЁїPCMЁзЁїCDBСНжжЃЌШЛКѓРћгУБпЕФЖдгІБШжЕЧѓГіЕузјБъЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉАбЕуAЃЈ3ЃЌ1ЃЉЃЌЕуCЃЈ0ЃЌ4ЃЉДњШыЖўДЮКЏЪ§y=Љx2+bx+cЕУЃЌ
![]() НтЕУ
НтЕУ![]() ЁрЖўДЮКЏЪ§НтЮіЪНЮЊy=Љx2+2x+4ЃЌ ХфЗНЕУy=ЉЃЈxЉ1ЃЉ2+5ЃЌ
ЁрЖўДЮКЏЪ§НтЮіЪНЮЊy=Љx2+2x+4ЃЌ ХфЗНЕУy=ЉЃЈxЉ1ЃЉ2+5ЃЌ
ЁрЕуMЕФзјБъЮЊЃЈ1ЃЌ5ЃЉЃЛ
ЃЈ2ЃЉЩшжБЯпACНтЮіЪНЮЊy=kx+bЃЌАбЕуAЃЈ3ЃЌ1ЃЉЃЌCЃЈ0ЃЌ4ЃЉДњШыЕУЃЌ![]() НтЕУЃК
НтЕУЃК![]()
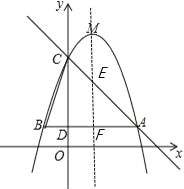
ЁржБЯпACЕФНтЮіЪНЮЊy=Љx+4ЃЌШчЭМЫљЪОЃЌЖдГЦжсжБЯпx=1гыЁїABCСНБпЗжБ№НЛгкЕуEЁЂЕуF
Абx=1ДњШыжБЯпACНтЮіЪНy=Љx+4НтЕУy=3ЃЌдђЕуEзјБъЮЊЃЈ1ЃЌ3ЃЉЃЌЕуFзјБъЮЊЃЈ1ЃЌ1ЃЉ
Ёр1ЃМ5ЉmЃМ3ЃЌНтЕУ2ЃМmЃМ4ЃЛ
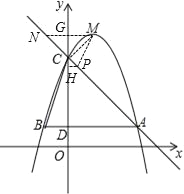
ЃЈ3ЃЉСЌНгMCЃЌзїMGЁЭyжсВЂбгГЄНЛACгкЕуNЃЌдђЕуGзјБъЮЊЃЈ0ЃЌ5ЃЉ ЁпMG=1ЃЌGC=5Љ4=1
ЁрMC=![]() =
=![]() ЃЌ Абy=5ДњШыy=Љx+4НтЕУx=Љ1ЃЌдђЕуNзјБъЮЊЃЈЉ1ЃЌ5ЃЉЃЌ
ЃЌ Абy=5ДњШыy=Љx+4НтЕУx=Љ1ЃЌдђЕуNзјБъЮЊЃЈЉ1ЃЌ5ЃЉЃЌ
ЁпNG=GCЃЌGM=GCЃЌ ЁрЁЯNCG=ЁЯGCM=45ЁуЃЌ ЁрЁЯNCM=90ЁуЃЌ
гЩДЫПЩжЊЃЌШєЕуPдкACЩЯЃЌдђЁЯMCP=90ЁуЃЌдђЕуDгыЕуCБиЮЊЯрЫЦШ§НЧаЮЖдгІЕу
ЂйШєгаЁїPCMЁзЁїBDCЃЌдђга![]()
ЁпBD=1ЃЌCD=3ЃЌ ЁрCP=![]() =
=![]() =
=![]() ЃЌ ЁпCD=DA=3ЃЌ ЁрЁЯDCA=45ЁуЃЌ
ЃЌ ЁпCD=DA=3ЃЌ ЁрЁЯDCA=45ЁуЃЌ
ШєЕуPдкyжсгвВрЃЌзїPHЁЭyжсЃЌ ЁпЁЯPCH=45ЁуЃЌCP=![]() ЁрPH=
ЁрPH=![]() =
=![]()
Абx=![]() ДњШыy=Љx4ЃЌНтЕУy=
ДњШыy=Љx4ЃЌНтЕУy=![]() ЃЌ ЁрP1ЃЈ
ЃЌ ЁрP1ЃЈ![]() ЃЉЃЛ
ЃЉЃЛ
ЭЌРэПЩЕУЃЌШєЕуPдкyжсзѓВрЃЌдђАбx=Љ![]() ДњШыy=Љx+4ЃЌНтЕУy=
ДњШыy=Љx+4ЃЌНтЕУy=![]() ЁрP2ЃЈ
ЁрP2ЃЈ![]() ЃЉЃЛ
ЃЉЃЛ
ЂкШєгаЁїPCMЁзЁїCDBЃЌдђга![]() ЁрCP=
ЁрCP=![]() =3
=3![]() ЁрPH=3
ЁрPH=3![]() ЁТ
ЁТ![]() =3ЃЌ
=3ЃЌ
ШєЕуPдкyжсгвВрЃЌАбx=3ДњШыy=Љx+4ЃЌНтЕУy=1ЃЛ
ШєЕуPдкyжсзѓВрЃЌАбx=Љ3ДњШыy=Љx+4ЃЌНтЕУy=7
ЁрP3ЃЈ3ЃЌ1ЃЉЃЛP4ЃЈЉ3ЃЌ7ЃЉЃЎ
ЁрЫљгаЗћКЯЬтвтЕУЕуPзјБъга4ИіЃЌЗжБ№ЮЊP1ЃЈ![]() ЃЉЃЌP2ЃЈ
ЃЉЃЌP2ЃЈ![]() ЃЉЃЌP3ЃЈ3ЃЌ1ЃЉЃЌP4ЃЈЉ3ЃЌ7ЃЉЃЎ
ЃЉЃЌP3ЃЈ3ЃЌ1ЃЉЃЌP4ЃЈЉ3ЃЌ7ЃЉЃЎ


 ЕМбЇШЋГЬСЗДДгХбЕСЗЯЕСаД№АИ
ЕМбЇШЋГЬСЗДДгХбЕСЗЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЁїABCжаЃЌЁЯB=ЁЯC=36ЁуЃЌADЁЂAEШ§ЕШЗжЁЯAЃЌDЁЂEдкBCБпЩЯЃЌдђЦфжаЕФЯрЫЦШ§НЧаЮЃЈВЛАќКЌШЋЕШЃЉгаЃЈЁЁЁЁЃЉ
A.1ЖдB.2ЖдC.3ЖдD.4Жд
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌBDЪЧЁїABCЕФНЧЦНЗжЯпЃЌЙ§ЕуDзїDEЁЮBCНЛABгкЕуEЃЌDFЁЮABНЛBCгкЕуFЃЎ
ЃЈ1ЃЉЧѓжЄЃКЫФБпаЮBEDFЮЊСтаЮЃЛ
ЃЈ2ЃЉШчЙћЁЯA=90ЁуЃЌЁЯC=30ЁуЃЌBD=12ЃЌЧѓСтаЮBEDFЕФУцЛ§ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
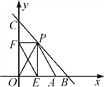
ЁОЬтФПЁПШчЭМЃЌжБЯпyЃНЃxЃЋ10гыxжсЁЂyжсЗжБ№НЛгкЕуBЃЌCЃЌЕуAЕФзјБъЮЊ(8ЃЌ0)ЃЌP(xЃЌy)ЪЧжБЯпyЃНЃxЃЋ10дкЕквЛЯѓЯоФкЕФвЛИіЖЏЕуЃЎ
(1)ЧѓЁїOPAЕФУцЛ§SгыxЕФКЏЪ§НтЮіЪНЃЌВЂаДГіздБфСПxЕФШЁжЕЗЖЮЇЃЛ
(2)Й§ЕуPзїPEЁЭxжсгкЕуEЃЌзїPFЁЭyжсгкЕуFЃЌСЌНгEFЃЌЪЧЗёДцдквЛЕуPЪЙЕУEFЕФГЄзюаЁЃЌШєДцдкЃЌЧѓГіEFЕФзюаЁжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдк![]() КЭ
КЭ![]() жаЃЌ
жаЃЌ![]() гы
гы![]() НЛгкЕуEЃЌЯжгаШ§ИіЬѕМўЃКЂй
НЛгкЕуEЃЌЯжгаШ§ИіЬѕМўЃКЂй![]() ЃЛЂк
ЃЛЂк![]() ЃЌЂл
ЃЌЂл![]() ЃЌЧыФуДгШ§ИіЬѕМўжабЁГіСНИізїЮЊЬѕМўЃЌСэвЛИізїЮЊНсТлЃЌзщГЩвЛИіецУќЬтЃЌВЂИјгшжЄУїЃЎ
ЃЌЧыФуДгШ§ИіЬѕМўжабЁГіСНИізїЮЊЬѕМўЃЌСэвЛИізїЮЊНсТлЃЌзщГЩвЛИіецУќЬтЃЌВЂИјгшжЄУїЃЎ
ЃЈ1ЃЉЬѕМўЪЧ ______ ЃЛНсТлЪЧ ______ (ЬюађКХ)ЃЛ
ЃЈ2ЃЉжЄУїЃК
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛДЮКЏЪ§y=ax+bЃЈaЁй0ЃЉЁЂЖўДЮКЏЪ§y=ax2+bxКЭЗДБШР§КЏЪ§y=![]() ЃЈkЁй0ЃЉдкЭЌвЛжБНЧзјБъЯЕжаЕФЭМЯѓШчЭМЫљЪОЃЌAЕуЕФзјБъЮЊЃЈ-2ЃЌ0ЃЉЃЌдђЯТСаНсТлжаЃЌе§ШЗЕФЪЧЃЈЁЁЁЁЃЉ
ЃЈkЁй0ЃЉдкЭЌвЛжБНЧзјБъЯЕжаЕФЭМЯѓШчЭМЫљЪОЃЌAЕуЕФзјБъЮЊЃЈ-2ЃЌ0ЃЉЃЌдђЯТСаНсТлжаЃЌе§ШЗЕФЪЧЃЈЁЁЁЁЃЉ

AЃЎb=2a+k BЃЎa=b+k CЃЎaЃОbЃО0 DЃЎaЃОkЃО0
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
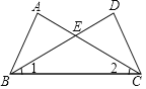
ЁОЬтФПЁПШчЭМЃЌABЮЊЁбOЕФжБОЖЃЌCЃЌEЮЊЁбOЩЯЕФСНЕуЃЌACЦНЗжЁЯEABЃЌCDЁЭAEгкDЃЎ
ЃЈ1ЃЉЧѓжЄЃКCDЮЊЁбOЕФЧаЯпЃЛ
ЃЈ2ЃЉЙ§ЕуCзїCFЁЭABгкFЃЌШчЭМ2ЃЌХаЖЯCFКЭAFЃЌDEжЎМфЕФЪ§СПЙиЯЕЃЌВЂжЄУїжЎЃЛ
ЃЈ3ЃЉШєAD-OA=1.5ЃЌAC=3![]() ЃЌЧѓЭМжавѕгАВПЗжЕФУцЛ§ЃЎ
ЃЌЧѓЭМжавѕгАВПЗжЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
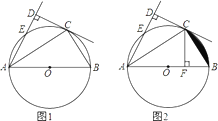
ЁОЬтФПЁПЃЈ6ЗжЃЉШчЭМЂйЫљЪОЃЌНЋжБГпАкЗХдкШ§НЧАхABCЩЯЃЌЪЙжБГпгыШ§НЧАхЕФБпЗжБ№НЛгкЕуDЃЌEЃЌFЃЌGЃЌСПЕУЁЯCGD=42ЁуЁЃ
ЃЈ1ЃЉЧѓЁЯCEFЕФЖШЪ§ЃЛ
ЃЈ2ЃЉНЋжБГпЯђЯТЦНвЦЃЌЪЙжБГпЕФБпдЕЭЈЙ§Ш§НЧАхЕФЖЅЕуBЃЌНЛACБпгкЕуHЃЌШчЭМЂкЫљЪОЃЎЕуHЃЌBдкжБГпЩЯЕФЖСЪ§ЗжБ№ЮЊ4ЃЌ13ЃЎ4ЃЌЧѓBCЕФГЄЃЈНсЙћБЃСєСНЮЛаЁЪ§ЃЉЃЎ
ЃЈВЮПМЪ§ОнЃКsin42ЁуЁж0ЃЎ67ЃЌcos42ЁуЁж0ЃЎ74ЃЌtan42ЁуЁж0ЃЎ90ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌОиаЮABCDЕФЖдНЧЯпACЁЂBDЯрНЛгкЕуOЃЌABЃН4ЃЌBCЃН8ЃЌЙ§ЕуOзїOEЁЭACНЛADгкЕуEЃЌдђAEЕФГЄЮЊ________ЃЎ
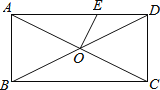
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com