
 ��ͼ����֪������y=-x2+bx+c��x�ύ��A��-1��0����B��3��0�����㣬��y�ύ�ڵ�C�������ߵĶԳ����������߽��ڵ�P����ֱ��BC�ཻ�ڵ�M������PB��
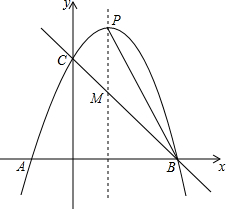
��ͼ����֪������y=-x2+bx+c��x�ύ��A��-1��0����B��3��0�����㣬��y�ύ�ڵ�C�������ߵĶԳ����������߽��ڵ�P����ֱ��BC�ཻ�ڵ�M������PB������ ��1����A��-1��0����B��3��0���������y=-x2+bx+c������������ߵĽ���ʽ��
��2����D��t��-t2+2t+3��������D��DH��x�ᣬ����S��BCD=S����OCDH+S��BDH-S��BOC=-$\frac{3}{2}$t2+$\frac{9}{2}$t���������D�����꼰��BCD��������ֵ��
��3�������P��BCƽ�е�ֱ���������ߵĽ���ΪQ������ֱ��BC�Ľ���ʽΪy=-x+3������P��BCƽ�е�ֱ��Ϊy=-x+5����Q������Ϊ��2��3��������PM�Ľ���ʽΪ��x=1��ֱ��BC�Ľ���ʽΪy=-x+3����M������Ϊ��1��2������PM��x�ύ�ڵ�E���������E��BCƽ�е�ֱ��Ϊy=-x+1������$\left\{\begin{array}{l}{y=-x+1}\\{y=-{x}^{2}+2x+3}\end{array}\right.$�õ�Q������Ϊ��$\frac{3+\sqrt{17}}{2}$��-$\frac{1+\sqrt{17}}{2}$������$\frac{3-\sqrt{17}}{2}$��-$\frac{1-\sqrt{17}}{2}$����
��� �⣺��1����$\left\{\begin{array}{l}{-1-b+c=0}\\{-9+3b+c=0}\end{array}\right.$��$\left\{\begin{array}{l}{b=2}\\{c=3}\end{array}\right.$���������ߵĽ���ʽΪy=-x2+2x+3��
��2����D��t��-t2+2t+3��������D��DH��x�ᣬ
��S��BCD=S����OCDH+S��BDH-S��BOC=$\frac{1}{2}$��-t2+2t+3+3��t+$\frac{1}{2}$��3-t����-t2+2t+3��-$\frac{1}{2}$��3��3=-$\frac{3}{2}$t2+$\frac{9}{2}$t��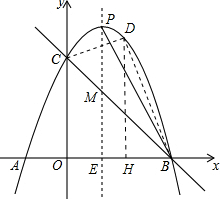
��-$\frac{3}{2}$��0��
�൱t=-$\frac{\frac{9}{2}}{2����-\frac{3}{2}��}$=$\frac{3}{2}$ʱ��D�������ǣ�$\frac{3}{2}$��$\frac{15}{4}$������BCD��������ֵ��$\frac{27}{8}$��
��3�������P��BCƽ�е�ֱ���������ߵĽ���ΪQ��
��P�������Ϊ��1��4����ֱ��BC�Ľ���ʽΪy=-x+3��
�����P��BCƽ�е�ֱ��Ϊy=-x+5��
��$\left\{\begin{array}{l}{y=-x+5}\\{y=-{x}^{2}+2x+3}\end{array}\right.$��Q��������2��3����
��PM�Ľ���ʽΪx=1��ֱ��BC�Ľ���ʽΪy=-x+3��
��M��������1��2����
��PM��x�ύ�ڵ�E��
��PM=EM=2��
�����E��BCƽ�е�ֱ��Ϊy=-x+1��
��$\left\{\begin{array}{l}{y=-x+1}\\{y=-{x}^{2}+2x+3}\end{array}\right.$��$\left\{\begin{array}{l}{x=\frac{3+\sqrt{17}}{2}}\\{y=-\frac{1+\sqrt{17}}{2}}\end{array}\right.$��$\left\{\begin{array}{l}{x=\frac{3-\sqrt{17}}{2}}\\{y=-\frac{1-\sqrt{17}}{2}}\end{array}\right.$��
���Q��������$\frac{3+\sqrt{17}}{2}$��-$\frac{1+\sqrt{17}}{2}$������$\frac{3-\sqrt{17}}{2}$��-$\frac{1-\sqrt{17}}{2}$����
��ʹ�á�QMB���PMB�������ȵĵ�Q������Ϊ��2��3������$\frac{3+\sqrt{17}}{2}$��-$\frac{1+\sqrt{17}}{2}$������$\frac{3-\sqrt{17}}{2}$��-$\frac{1-\sqrt{17}}{2}$����
���� ���⿼���˶��κ����ۺϣ��õ���֪ʶ���Ƕ��κ�����ͼ�������ʡ����������ε������ֱ���������ߵĽ��㣬�ؼ������������ߣ�����������������е�����꣮


 ����������ϵ�д�
����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
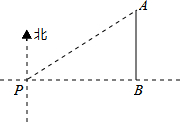 ��ͼ��һ�Һ���λ�ڵ���P�ı�ƫ��55�㷽�������2����ĵ�A����������������Ϸ����е����������������ֺ��еľ���AB���ǣ�������
��ͼ��һ�Һ���λ�ڵ���P�ı�ƫ��55�㷽�������2����ĵ�A����������������Ϸ����е����������������ֺ��еľ���AB���ǣ�������| A�� | 2���� | B�� | 2sin55�㺣�� | C�� | 2cos55�㺣�� | D�� | 2tan55�㺣�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
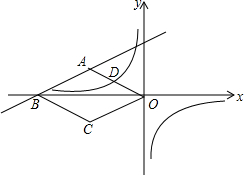 ��ͼ����ƽ��ֱ������ϵ�У��ı���ABCO�����Σ�B��O��x�Ḻ�����ϣ�AO=$\sqrt{5}$��tan��AOB=$\frac{1}{2}$��һ�κ���y=k1x+b��ͼ���A��B���㣬����������y=$\frac{{k}_{2}}{x}$��ͼ���OA���е�D��
��ͼ����ƽ��ֱ������ϵ�У��ı���ABCO�����Σ�B��O��x�Ḻ�����ϣ�AO=$\sqrt{5}$��tan��AOB=$\frac{1}{2}$��һ�κ���y=k1x+b��ͼ���A��B���㣬����������y=$\frac{{k}_{2}}{x}$��ͼ���OA���е�D���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
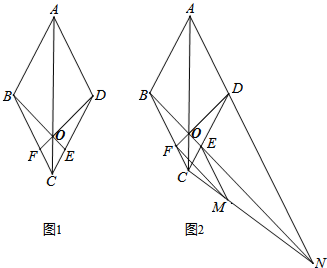
 ��ͼ���ڱ߳�Ϊ2��������ABCD�У�G��AD�ӳ����ϵ�һ�㣬��DG=AD������M��A���������ÿ��1����λ���ٶ�����A��C��G��·����G�������˶���M����A��G�غϣ������˶�ʱ��Ϊt�룬����BM���ӳ�AG��N��
��ͼ���ڱ߳�Ϊ2��������ABCD�У�G��AD�ӳ����ϵ�һ�㣬��DG=AD������M��A���������ÿ��1����λ���ٶ�����A��C��G��·����G�������˶���M����A��G�غϣ������˶�ʱ��Ϊt�룬����BM���ӳ�AG��N���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 5.49��1018 | B�� | 5.49��1016 | C�� | 5.49��1015 | D�� | 5.49��1014 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
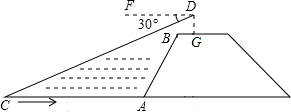 ��ͼ��С��վ�ںӰ��ϵ�G�㣬����������һС���ش�ֱ�ڰ��ߵķ���������ʱ�����С��C�ĸ����ǡ�FDC=30�㣬��С�����۾������ľ�����1.6�ף�BG=0.7�ף�BGƽ����AC���ڵ�ֱ�ߣ�ӭˮ��i=4��3���³�AB=8�ף���A��B��C��D��F��G��ͬһƽ���ڣ����ʱС��C�����ߵľ���CA�ij�Ϊ8$\sqrt{3}$-5.5�ף�������������ţ�
��ͼ��С��վ�ںӰ��ϵ�G�㣬����������һС���ش�ֱ�ڰ��ߵķ���������ʱ�����С��C�ĸ����ǡ�FDC=30�㣬��С�����۾������ľ�����1.6�ף�BG=0.7�ף�BGƽ����AC���ڵ�ֱ�ߣ�ӭˮ��i=4��3���³�AB=8�ף���A��B��C��D��F��G��ͬһƽ���ڣ����ʱС��C�����ߵľ���CA�ij�Ϊ8$\sqrt{3}$-5.5�ף�������������ţ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com