
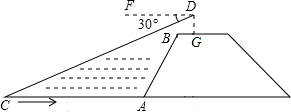
 如图,小华站在河岸上的G点,看见河里有一小船沿垂直于岸边的方向划过来.此时,测得小船C的俯角是∠FDC=30°,若小华的眼睛与地面的距离是1.6米,BG=0.7米,BG平行于AC所在的直线,迎水坡i=4:3,坡长AB=8米,点A、B、C、D、F、G在同一平面内,则此时小船C到岸边的距离CA的长为8$\sqrt{3}$-5.5米.(结果保留根号)
如图,小华站在河岸上的G点,看见河里有一小船沿垂直于岸边的方向划过来.此时,测得小船C的俯角是∠FDC=30°,若小华的眼睛与地面的距离是1.6米,BG=0.7米,BG平行于AC所在的直线,迎水坡i=4:3,坡长AB=8米,点A、B、C、D、F、G在同一平面内,则此时小船C到岸边的距离CA的长为8$\sqrt{3}$-5.5米.(结果保留根号) 分析 把AB和CD都整理为直角三角形的斜边,利用坡度和勾股定理易得点B和点D到水面的距离,进而利用俯角的正切值可求得CH长度.CH-AE=EH即为AC长度.
解答 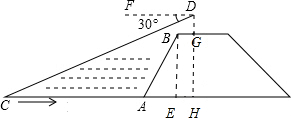 解:过点B作BE⊥AC于点E,延长DG交CA于点H,得Rt△ABE和矩形BEHG.
解:过点B作BE⊥AC于点E,延长DG交CA于点H,得Rt△ABE和矩形BEHG.
∵i=$\frac{BE}{AE}$=$\frac{4}{3}$,AB=8米,
∴BE=$\frac{32}{5}$,AE=$\frac{24}{5}$.
∵DG=1.6,BG=0.7,
∴DH=DG+GH=1.6+$\frac{32}{5}$=8,
AH=AE+EH=$\frac{24}{5}$+0.7=5.5.
在Rt△CDH中,
∵∠C=∠FDC=30°,DH=8,tan30°=$\frac{DH}{CH}$=$\frac{\sqrt{3}}{3}$,
∴CH=8$\sqrt{3}$.
又∵CH=CA+5.5,
即8$\sqrt{3}$=CA+5.5,
∴CA=8$\sqrt{3}$-5.5(米).
答:CA的长约是(8$\sqrt{3}$-5.5)米.
点评 此题考查了俯角与坡度的知识.注意构造所给坡度和所给锐角所在的直角三角形是解决问题的难点,利用坡度和三角函数求值得到相应线段的长度是解决问题的关键.


科目:初中数学 来源: 题型:填空题
 观光塔是潍坊市区的标志性建筑,为测量其高度,如图,一人先在附近一楼房的底端A点处观测观光塔顶端C处的仰角是60°,然后爬到该楼房顶端B点处观测观光塔底部D处的俯角是30°.已知楼房高AB约是45m,根据以上观测数据可求观光塔的高CD是135m.
观光塔是潍坊市区的标志性建筑,为测量其高度,如图,一人先在附近一楼房的底端A点处观测观光塔顶端C处的仰角是60°,然后爬到该楼房顶端B点处观测观光塔底部D处的俯角是30°.已知楼房高AB约是45m,根据以上观测数据可求观光塔的高CD是135m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
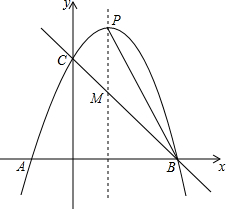 如图,已知抛物线y=-x2+bx+c与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C,抛物线的对称轴与抛物线交于点P、与直线BC相交于点M,连接PB.
如图,已知抛物线y=-x2+bx+c与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C,抛物线的对称轴与抛物线交于点P、与直线BC相交于点M,连接PB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,将?ABCD的AD边延长至点E,使DE=$\frac{1}{2}$AD,连接CE,F是BC边的中点,连接FD.
如图,将?ABCD的AD边延长至点E,使DE=$\frac{1}{2}$AD,连接CE,F是BC边的中点,连接FD.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
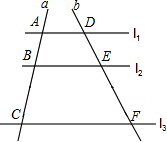 如图,l1∥l2∥l3,直线a,b与l1、l2、l3分别相交于A、B、C和点D、E、F.若$\frac{AB}{BC}$=$\frac{2}{3}$,DE=4,则EF的长是( )
如图,l1∥l2∥l3,直线a,b与l1、l2、l3分别相交于A、B、C和点D、E、F.若$\frac{AB}{BC}$=$\frac{2}{3}$,DE=4,则EF的长是( )| A. | $\frac{8}{3}$ | B. | $\frac{20}{3}$ | C. | 6 | D. | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | “任意画出一个等边三角形,它是轴对称图形”是随机事件 | |
| B. | “任意画出一个平行四边形,它是中心对称图形”是必然事件 | |
| C. | “概率为0.0001的事件”是不可能事件 | |
| D. | 任意掷一枚质地均匀的硬币10次,正面向上的一定是5次 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com