
 如图,在边长为2的正方形ABCD中,G是AD延长线上的一点,且DG=AD,动点M从A点出发,以每秒1个单位的速度沿着A→C→G的路线向G点匀速运动(M不与A,G重合),设运动时间为t秒,连接BM并延长AG于N.
如图,在边长为2的正方形ABCD中,G是AD延长线上的一点,且DG=AD,动点M从A点出发,以每秒1个单位的速度沿着A→C→G的路线向G点匀速运动(M不与A,G重合),设运动时间为t秒,连接BM并延长AG于N.分析 (1)四种情况:当点M为AC的中点时,AM=BM;当点M与点C重合时,AB=BM;当点M在AC上,且AM=2时,AM=AB;当点M在AC上,且AM=BM时,AM=$\sqrt{2}$时;当点M为CG的中点时,AM=BM;△ABM为等腰三角形;
(2)在AB上截取AK=AN,连接KN;由正方形的性质得出∠ADC=90°,AB=AD,∠CDG=90°,得出BK=DN,先证出∠BKN=∠NDH,再证出∠ABN=∠DNH,由ASA证明△BNK≌△NHD,得出BN=NH即可;
(3)①当M在AC上时,即0<t≤2$\sqrt{2}$时,△AMF为等腰直角三角形,得出AF=FM=$\frac{\sqrt{2}}{2}$t,求出S=$\frac{1}{2}$AF•FM=$\frac{1}{4}$t2;当t=2$\sqrt{2}$时,即可求出S的最大值;
②当M在CG上时,即2$\sqrt{2}$<t<4$\sqrt{2}$时,先证明△ACD≌△GCD,得出∠ACD=∠GCD=45°,求出∠ACM=90°,证出△MFG为等腰直角三角形,得出FG=MG•cos45°=4-$\frac{\sqrt{2}}{2}$t,得出S=S△ACG-S△CMJ-S△FMG,S为t的二次函数,即可求出结果.
解答 (1)解:存在;当点M为AC的中点时,AM=BM,则△ABM为等腰三角形;
当点M与点C重合时,AB=BM,则△ABM为等腰三角形;
当点M在AC上,且AM=2时,AM=AB,则△ABM为等腰三角形;
当点M在AC上,且AM=BM时,AM=$\frac{1}{2}$AC=$\frac{1}{2}$×2$\sqrt{2}$=$\sqrt{2}$时,则△ABM为等腰三角形;
当点M为CG的中点时,AM=BM,则△ABM为等腰三角形;
(2)证明:在AB上截取AK=AN,连接KN;如图1所示: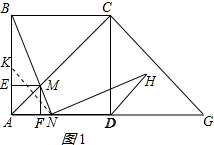 ∵四边形ABCD是正方形,
∵四边形ABCD是正方形,
∴∠ADC=90°,AB=AD,
∴∠CDG=90°,
∵BK=AB-AK,ND=AD-AN,
∴BK=DN,
∵DH平分∠CDG,
∴∠CDH=45°,
∴∠NDH=90°+45°=135°,
∴∠BKN=180°-∠AKN=135°,
∴∠BKN=∠NDH,
在Rt△ABN中,∠ABN+∠ANB=90°,
又∵BN⊥NH,
即∠BNH=90°,
∴∠ANB+∠DNH=180°-∠BNH=90°,
∴∠ABN=∠DNH,
在△BNK和△NHD中,
$\left\{\begin{array}{l}{∠ABN=∠DNH}&{\;}\\{BK=DN}&{\;}\\{∠BKN=∠NDH}&{\;}\end{array}\right.$,
∴△BNK≌△NHD(ASA),
∴BN=NH;
(3)解:①当M在AC上时,即0<t≤2$\sqrt{2}$时,△AMF为等腰直角三角形,
∵AM=t,
∴AF=FM=$\frac{\sqrt{2}}{2}$t,
∴S=$\frac{1}{2}$AF•FM=$\frac{1}{2}$×$\frac{\sqrt{2}}{2}$t×$\frac{\sqrt{2}}{2}$t=$\frac{1}{4}$t2;
当t=2$\sqrt{2}$时,S的最大值=$\frac{1}{2}$×(2$\sqrt{2}$)2=2;
②当M在CG上时,即2$\sqrt{2}$<t<4$\sqrt{2}$时,如图2所示: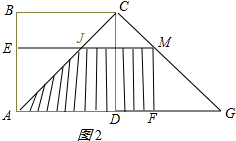 CM=t-AC=t-2$\sqrt{2}$,MG=4$\sqrt{2}$-t,
CM=t-AC=t-2$\sqrt{2}$,MG=4$\sqrt{2}$-t,
在△ACD和△GCD中,
$\left\{\begin{array}{l}{AD=DG}&{\;}\\{∠ADC=∠CDG}&{\;}\\{CD=CD}&{\;}\end{array}\right.$,
∴△ACD≌△GCD(SAS),
∴∠ACD=∠GCD=45°,
∴∠ACM=∠ACD+∠GCD=90°,
∴∠G=90°-∠GCD=45°,
∴△MFG为等腰直角三角形,
∴FG=MG•cos45°=(4$\sqrt{2}$-t)•$\frac{\sqrt{2}}{2}$=4-$\frac{\sqrt{2}}{2}$t,
∴S=S△ACG-S△CMJ-S△FMG=$\frac{1}{2}$×4×2-$\frac{1}{2}$×CM×CM-$\frac{1}{2}$×FG×FG
=4-$\frac{1}{2}$(t-2$\sqrt{2}$)2-$\frac{1}{2}$(4-$\frac{\sqrt{2}}{2}t$)2=-$\frac{3}{4}{t}^{2}$+4$\sqrt{2}$t-8
=-$\frac{3}{4}$(t-$\frac{8}{3}\sqrt{2}$)2+$\frac{8}{3}$,
∴当t=$\frac{8}{3}\sqrt{2}$时,S的最大值为$\frac{8}{3}$.
点评 本题是相似形综合题目,考查了等腰三角形的判定、正方形的性质、全等三角形的判定与性质、等腰直角三角形的判定与性质、三角函数以及三角形面积的计算等知识;本题难度较大,综合性强,特别是(3)中,需要进行分类讨论,通过证明三角形全等和等腰直角三角形才能得出结果.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
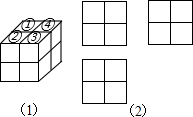 如图,用八个同样大小的小立方体搭成一个大立方体,小明从如图(1)上面的四个小立方体(①②③④)中取走了任意两个后,得到的新几何体的三视图如图(2)所示的概率为$\frac{1}{3}$.
如图,用八个同样大小的小立方体搭成一个大立方体,小明从如图(1)上面的四个小立方体(①②③④)中取走了任意两个后,得到的新几何体的三视图如图(2)所示的概率为$\frac{1}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
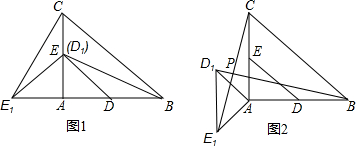
 如图,某塔观光层的最外沿点E为蹦极项目的起跳点.已知点E离塔的中轴线AB的距离OE为10米,塔高AB为123米(AB垂直地面BC),在地面C处测得点E的仰角α=45°,从点C沿CB方向前行40米到达D点,在D处测得塔尖A的仰角β=60°,求点E离地面的高度EF.(结果精确到1米,参考数据$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)
如图,某塔观光层的最外沿点E为蹦极项目的起跳点.已知点E离塔的中轴线AB的距离OE为10米,塔高AB为123米(AB垂直地面BC),在地面C处测得点E的仰角α=45°,从点C沿CB方向前行40米到达D点,在D处测得塔尖A的仰角β=60°,求点E离地面的高度EF.(结果精确到1米,参考数据$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,∠B、∠C的平分线BE,CD相交于点F,∠ABC=42°,∠A=60°,则∠BFC=( )
如图,在△ABC中,∠B、∠C的平分线BE,CD相交于点F,∠ABC=42°,∠A=60°,则∠BFC=( )| A. | 118° | B. | 119° | C. | 120° | D. | 121° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
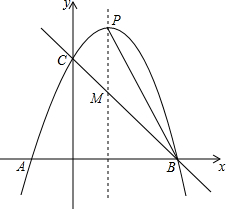 如图,已知抛物线y=-x2+bx+c与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C,抛物线的对称轴与抛物线交于点P、与直线BC相交于点M,连接PB.
如图,已知抛物线y=-x2+bx+c与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C,抛物线的对称轴与抛物线交于点P、与直线BC相交于点M,连接PB.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-3mn)2=-6m2n2 | B. | 4x4+2x4+x4=6x4 | C. | (xy)2÷(-xy)=-xy | D. | (a-b)(-a-b)=a2-b2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,将?ABCD的AD边延长至点E,使DE=$\frac{1}{2}$AD,连接CE,F是BC边的中点,连接FD.
如图,将?ABCD的AD边延长至点E,使DE=$\frac{1}{2}$AD,连接CE,F是BC边的中点,连接FD.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 圆锥的俯视图是圆 | |
| B. | 对角线互相垂直平分的四边形是菱形 | |
| C. | 任意一个等腰三角形是钝角三角形 | |
| D. | 周长相等的正方形、长方形、圆,这三个几何图形中,圆面积最大 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com