Question

10．如图，矩形ABCD中，点B与原点重合，点D（8，6），AE⊥BD，△AEB沿着y轴翻折得到△AFB，将△AFB绕着点B顺时针旋转α（0°＜α＜90°）得到△BF′A′，直线F′A′与线段AB、AE分别交于点M、N，当MN=MA时，△BF′A′与△AEB重叠部分的面积为$\frac{108}{25}$．

Answer 1

分析 依题意画出图形，利用相似三角形对应边成比例求解．

解答 解：在矩形ABCD中，∴AD=8，AB=6，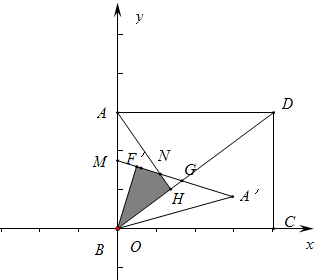
∴DO=$\sqrt{A{B}^{2}+A{D}^{2}}$=10，
∵AE⊥OD，
∴$\frac{1}{2}$•AO•AD=$\frac{1}{2}$•OD•AE，
∴AE=$\frac{24}{5}$，
∴OE=OF′=$\sqrt{A{O}^{2}-A{E}^{2}}$=$\frac{18}{5}$
∵AM=MN，
∴∠MAN=∠ANM，
∵∠ENG+∠NGE=90°，∠ANM=∠ENG，
∴∠AOE=∠OGF′，
∵∠AEO=∠OF′G=90°，
∴△AEO∽△OF′G，
∴$\frac{AE}{OF′}=\frac{AO}{OG}$得OG=$\frac{9}{2}$，
∴F′G=$\sqrt{O{G}^{2}-OF{′}^{2}}$=$\frac{27}{10}$，EG=$\frac{9}{10}$，
由△NEG∽△AEO，得$\frac{NE}{AE}=\frac{EG}{EO}$，
∴NE=$\frac{6}{5}$，
∴S_重合=S_△OGF′-S_△NEG=$\frac{1}{2}$$•\frac{18}{5}$•$\frac{27}{10}$-$\frac{1}{2}$•$\frac{9}{10}$•$\frac{6}{5}$=$\frac{108}{25}$．
故答案为$\frac{108}{25}$．

点评 本题考查了旋转、矩形的性质、勾股定理、等腰三角形的性质和判定、相似三角形的性质和判定等知识点，解题关键是正确画出图形，充分利用相似三角形对应边成比例解决问题．