Question

平面直角坐标第xoy中，A点的坐标为（0，5）．B、C分别是x轴、y轴上的两个动点，C从A出发，沿y轴负半轴方向以1个单位/秒的速度向点O运动，点B从O出发，沿x轴正半轴方向以1个单位/秒的速度运动．设运动时间为t秒，点D是线段OB上一点，且BD=OC．点E是第一象限内一点，且AEDB．

（1）当t=4秒时，求过E、D、B三点的抛物线解析式．

（2）当0＜t＜5时，（如图甲），∠ECB的大小是否随着C、B的变化而变化？如果不变，求出它的大小．

（3）求证：∠APC=45°

（4）当t＞5时，（如图乙）∠APC的大小还是45°吗？请说明理由．

 

 

Answer 1

（1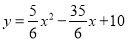）；（2）∠ECB的大小不变．90°；（3）证明见解析；（4）∠APC＞45°．

【解析】

试题分析：（1）当t=4时，知AC=OB=4，进而知OC=1，由BD=OC,AE∥DB，AE=BD可求AE=DB=OC=1,点E、点D、点B的坐标即可确定。再设出抛物线的解析式y=ax2+bx+c，将三点坐标代入即可求出a、b、c的值；

（2）连接CE，可证∠ECB=90°;

（3）由（2）可知：△ECB是等腰直角三角形，继而可证四边形ADBE是平行四边形，从而∠APC=∠EBC=45°；

（4）如图，在第二象限取点F，作AF∥BD，AF=BD，连接CF、BF．易得Rt△ACF≌Rt△OBC，再证△BCF是等腰直角三角形，由三角形的一个外角大于与它不相邻的内角知∠APC＞45°．

（1）当t=4秒时，AC=OB=4，由A（0，5）得C（0，1），即OC=1．

又BD=OC，AE DB，

∴AE=DB=OC=1．

∴E（1，5）B（4，0），D（3，0）．

设过E、D、B三点的抛物线解析式为y=ax2+bx+c ，则有

,解得：；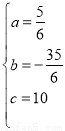

∴抛物线解析式为；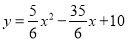

（2）（2）∠ECB的大小不变。

连接CE。易得Rt△ACE≌Rt△OBC（SAS）

∴CE=CB，∠ACE=∠OBC，∠AEC=∠OCB．

又∠ACE+∠AEC=90°，

∴∠ACE+∠OCB=90°

，∴∠ECB=90°．

（3）由（2）知，CE=CB，∠ECB=90°，

∴△ECB是等腰直角三角形．

∴∠EBC=45°，

又AEDB，

∴四边形ADBE是平行四边形．

∴AB∥EB．

∴∠APC=∠EBC=45°．

（4）当t＞5时，∠APC＞45°，理由如下：

如图，在第二象限取点F，作AFBD，连接CF、BF．

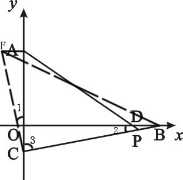
易得Rt△ACF≌Rt△OBC（SAS）

∴CF=CB，∠1=∠2．

又∠1+∠3=90°。∴∠2+∠3=90°即△BCF是等腰直角三角形．

∴∠CBF=45°，又∠APC＞∠CBF，

∴∠APC＞45°．

考点：1．二次函数关系式；2．三角形全等的判定与性质．