
【题目】如图,Rt△ABO的直角边OB在x轴上,OB=2,AB=1,将Rt△ABO绕点O顺时针旋转90°得到Rt△CDO,抛物线y=﹣![]() +bx+c经过A,C两点.
+bx+c经过A,C两点.
(1)求点A,C的坐标;
(2)求二次函数的解析式;
(3)连接AC,点P是抛物线上一点,直线OP把△AOC的周长分成相等的两部分,求点P的坐标.

【答案】(1)A(﹣2,1),C(1,2);(2)y=-![]() -
-![]() x+
x+![]() ;(3)(4,﹣12)或(﹣1,3)
;(3)(4,﹣12)或(﹣1,3)
【解析】
(1)根据线段OB、AB的长度易得点A的坐标,根据旋转的性质求得C点的坐标;
(2)根据待定系数法即可求得;
(3)由直线OP把△AOC的周长分成相等的两部分且OA=OC,知AQ=CQ,即点Q为AC的中点,从而得出点Q坐标,求得直线OP解析式,联立方程可得点P坐标.
解:(1)∵OB=2,AB=1,
∴A(﹣2,1),
将Rt△ABO绕点O顺时针旋转90°得到Rt△CDO,
∴C(1,2),
(2)∵抛物线y=﹣![]() +bx+c经过A,C两点,
+bx+c经过A,C两点,
∴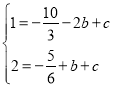 ,解得
,解得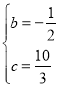
∴二次函数的解析式为y=﹣![]() ﹣
﹣![]() x+
x+![]() ;
;
(3)设OP与AC交于点Q,
∵OP将△AOC的周长分成相等的两部分,又OA=OC,OQ=OQ,
∴AQ=CQ,即Q为AC的中点,
∴Q(﹣![]() ,
,![]() ).
).
设直线OP的解析式为y=kx,把Q(﹣![]() ,
,![]() )代入y=kx,得
)代入y=kx,得![]() =﹣
=﹣![]() k,
k,
∴k=﹣3.
∴直线OP的解析式为y=﹣3x.
由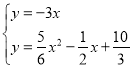 ,得
,得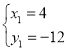 ,
,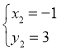 ,
,
∴P1(4,﹣12),P2(﹣1,3).


科目:初中数学 来源: 题型:
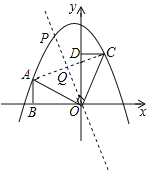
【题目】如图,在平面直角坐标系xOy中,A(4,0),B(0,3),C(4,3),I是△ABC的内心,将△ABC绕原点逆时针旋转90°后,I的对应点I'的坐标为( )
A. (﹣2,3) B. (﹣3,2) C. (3,﹣2) D. (2,﹣3)
查看答案和解析>>
科目:初中数学 来源: 题型:
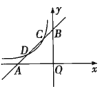
【题目】如图,已知直线![]() 与x轴、y轴分别交于点A,B,与双曲线
与x轴、y轴分别交于点A,B,与双曲线![]() 分别交于点C,D,且点C的坐标为
分别交于点C,D,且点C的坐标为![]() .
.
(1)分别求出直线、双曲线的函数表达式.
(2)求出点D的坐标.
(3)利用图象直接写出:当x在什么范围内取值时![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段AB=a,点P是AB中垂线MN上的一动点,过点P作直线CD∥AB.若在直线CD上存在点Q使得△ABQ为等腰三角形,且满足条件的点Q有且只有3个,则PM的长为_____.
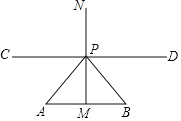
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l为正比例函数y=x的图象,点A1的坐标为(1,0),过点A1作x轴的垂线交直线l于点D1,以A1D1为边作正方形A1B1C1D1;过点C1作直线l的垂线,垂足为A2,交x轴于点B2,以A2B2为边作正方形A2B2C2D2;过点C2作x轴的垂线,垂足为A3,交直线l于点A3,以A3D3为边作正方形A3B3C3D3,…,按此规律操作下所得到的正方形A2019B2019C2019D2019的面积是_____.
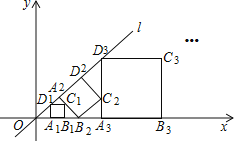
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小卖部从批发市场购进一批李子,在销售了部分李子之后,余下的每千克降价3元,直至全部售完.销售金额(元)与李子销售量(千克)之间的关系如图所示.若销售这批李子一共赢利220元,那么这批李子的进价是_____元.
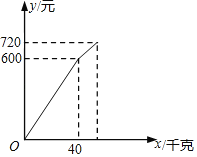
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点O(0,0),点A(1,0).已知抛物线y=x2+mx﹣2m(m是常数),顶点为P.
(Ⅰ)当抛物线经过点A时,求顶点P的坐标;
(Ⅱ)若点P在x轴下方,当∠AOP=45°时,若函数值y>0,求对应自变量x的取值范围;
(Ⅲ)无论m取何值,该抛物线都经过定点H.当∠AHP=45°时,求抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为早日实现脱贫奔小康的宏伟目标,我市结合本地丰富的山水资源,大力发展旅游业,王家庄在当地政府的支持下,办起了民宿合作社,专门接待游客,合作社共有80间客房.根据合作社提供的房间单价x(元)和游客居住房间数y(间)的信息,乐乐绘制出y与x的函数图象如图所示:
(1)求y与x之间的函数关系式;
(2)合作社规定每个房间价格不低于60元且不超过150元,对于游客所居住的每个房间,合作社每天需支出20元的各种费用,房价定为多少时,合作社每天获利最大?最大利润是多少?
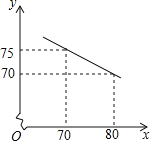
查看答案和解析>>
科目:初中数学 来源: 题型:
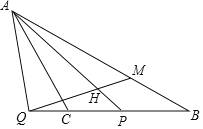
【题目】如图,已知等腰△ABC,∠ACB=120°,P是线段CB上一动点(与点C,B不重合),连接AP,延长BC至点Q,使得∠PAC=∠QAC,过点Q作射线QH交线段AP于H,交AB于点M,使得∠AHQ=60°.
(1)若∠PAC=α,求∠AMQ的大小(用含α的式子表示);
(2)用等式表示线段QC和BM之间的数量关系,并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com