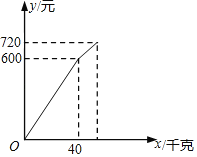
【题目】小卖部从批发市场购进一批李子，在销售了部分李子之后，余下的每千克降价3元，直至全部售完．销售金额（元）与李子销售量（千克）之间的关系如图所示．若销售这批李子一共赢利220元，那么这批李子的进价是_____元．
长江作业本同步练习册系列答案科目：初中数学 来源： 题型：
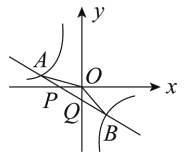
【题目】如图，已知直线
与
轴、
轴相交于
、
两点，与
的图象相交于
、
两点，连接
、
.给出下列结论：
①
；②
；③
；④不等式
的解集是
或
.
其中正确结论的序号是__________．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，已知抛物线的顶点为A（2，1），且经过原点O，与x轴的另一个交点为B．
（1）求抛物线的解析式；
（2）若点C在抛物线的对称轴上，点D在抛物线上，且以O、C、D、B四点为顶点的四边形为平行四边形，求D点的坐标；
（3）连接OA、AB，如图2，在x轴下方的抛物线上是否存在点P，使得△OBP与△OAB相似？若存在，求出P点的坐标；若不存在，说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知AB是⊙O的直径，弦CD⊥AB于点E．点P是劣弧
上任一点（不与点A，D重合），CP交AB于点M，AP与CD的延长相交于点F．
（1）设∠CPF＝α，∠BDC＝β，求证：α＝β+90°；
（2）若OE＝BE，设tan∠AFC＝x，
．①求∠APC的度数；
②求y关于x的函数表达式及自变量x的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，Rt△ABO的直角边OB在x轴上，OB＝2，AB＝1，将Rt△ABO绕点O顺时针旋转90°得到Rt△CDO，抛物线y＝﹣
+bx+c经过A，C两点．
（1）求点A，C的坐标；
（2）求二次函数的解析式；
（3）连接AC，点P是抛物线上一点，直线OP把△AOC的周长分成相等的两部分，求点P的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】知识背景：
当a＞0且x＞0时，因为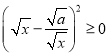
，所以x﹣2
≥0，从而
（当
，即x＝
时取等号）．
设函数y＝x+
（x＞0，a＞0），由上述结论可知：当x＝时，该函数有最小值2．
应用举例
已知函数为y1＝x（x＞0）与函数y2＝
（x＞0），则当x＝
时，y1+y2＝x+有最小值为2．
解决问题
（1）已知函数为y1＝x﹣1（x＞1）与函数y2＝（x﹣1）2+9（x＞1），当x取何值时，
有最小值？最小值是多少？
（2）已知某设备租赁使用成本包含以下三部分：一是设备的安装调试费用，共490元；二是设备的租赁使用费用，每天200元；三是设备的折旧费用，它与使用天数的平方成正比，比例系数为0．001．若设该设备的租赁使用天数为x天，则当x取何值时，该设备平均每天的租赁使用成本最低？最低是多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在
中，
,
,
为
边的高，点
在
轴上，点
在
轴上，点
在第一象限，若从原点出发，沿轴向右以每秒1个单位长的速度运动，则点随之沿轴下滑，并带动在平面内滑动，设运动时间为
秒，当到达原点时停止运动
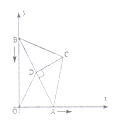
（1）连接
，线段的长随的变化而变化，当最大时，
______.
（2）当的边与坐标轴平行时，______.
查看答案和解析>>
科目：初中数学 来源： 题型：
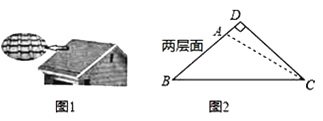
【题目】太阳能光伏建筑是现代绿色环保建筑之一，老张准备把自家屋顶改建成光伏瓦面，改建前屋顶截面△ABC如图2所示，BC=10米，∠ABC=∠ACB=36°，改建后顶点D在BA的延长线上，且∠BDC=90°，求改建后南屋面边沿增加部分AD的长．（结果精确到0.1米）
（参考数据：sin18°≈0.31，cos18°≈0.95．tan18°≈0.32，sin36°≈0.59．cos36°≈0.81，tan36°≈0.73）
查看答案和解析>>
科目：初中数学 来源： 题型：
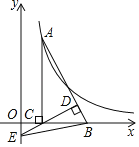
【题目】如图，点A在反比例函数y＝
（x＞0）的图象上，AC⊥x轴，垂足为C，B在OC延长线上，∠CAB＝30°，直线CD⊥AB，CD与AB和y轴交点分别为D，E，连接BE，△BCE的面积为1，则k的值是_______．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
