
【题目】知识背景:
当a>0且x>0时,因为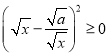 ,所以x﹣2
,所以x﹣2![]() ≥0,从而
≥0,从而![]() (当
(当![]() ,即x=
,即x=![]() 时取等号).
时取等号).
设函数y=x+![]() (x>0,a>0),由上述结论可知:当x=
(x>0,a>0),由上述结论可知:当x=![]() 时,该函数有最小值2
时,该函数有最小值2![]() .
.
应用举例
已知函数为y1=x(x>0)与函数y2=![]() (x>0),则当x=
(x>0),则当x=![]() 时,y1+y2=x+
时,y1+y2=x+![]() 有最小值为2
有最小值为2![]() .
.
解决问题
(1)已知函数为y1=x﹣1(x>1)与函数y2=(x﹣1)2+9(x>1),当x取何值时,![]() 有最小值?最小值是多少?
有最小值?最小值是多少?
(2)已知某设备租赁使用成本包含以下三部分:一是设备的安装调试费用,共490元;二是设备的租赁使用费用,每天200元;三是设备的折旧费用,它与使用天数的平方成正比,比例系数为0.001.若设该设备的租赁使用天数为x天,则当x取何值时,该设备平均每天的租赁使用成本最低?最低是多少元?
【答案】(1)x=4时![]() 有最小值,最小值是6;(2)当x取700时,该设备平均每天的租赁使用成本最低,最低是201.4元.
有最小值,最小值是6;(2)当x取700时,该设备平均每天的租赁使用成本最低,最低是201.4元.
【解析】
(1)通过对知识背景和应用举例的理解来解决即可;
(2)平均每天租赁使用成本=总成本÷总使用天数,先根据成本包括的三部分把总成本表示出来,然后除以总使用天数,根据知识背景即可求解.
(1)![]() =
=![]() =(x﹣1)+
=(x﹣1)+![]()
∵x>1,∴x﹣1>0
根据题意,当x﹣1=![]() =3时,
=3时,
![]() 有最小值2
有最小值2![]() =6,
=6,
∴x=4,
即x=4时![]() 有最小值,最小值是6;
有最小值,最小值是6;
(2)设该设备平均每天的租赁使用成本w元,
根据题意,得
w=(490+200x+0.001x2)÷x
=![]() +200+0.001x
+200+0.001x
所以当![]() =0.001x时,w有最小值,
=0.001x时,w有最小值,
w最小值为2![]() +200=201.4.
+200=201.4.
解得x=700或﹣700(舍去),
答:当x取700时,该设备平均每天的租赁使用成本最低,最低是201.4元.


科目:初中数学 来源: 题型:
【题目】如图,BD为△ABC外接圆⊙O的直径,且∠BAE=∠C.
(1)求证:AE与⊙O相切于点A;
(2)若AE∥BC,BC=2![]() ,AC=2
,AC=2![]() ,求AD的长.
,求AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,AB为直径,点M为AB延长线上的一点,MC与⊙O相切于点C,圆周上有另一点D与点C分居直径AB两侧,且使得MC=MD=AC,连接AD.现有下列结论:①MD与⊙O相切;②四边形ACMD是菱形;③AB=MO;④∠ADM=120°,其中正确的结论有( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD,等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.
(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小卖部从批发市场购进一批李子,在销售了部分李子之后,余下的每千克降价3元,直至全部售完.销售金额(元)与李子销售量(千克)之间的关系如图所示.若销售这批李子一共赢利220元,那么这批李子的进价是_____元.
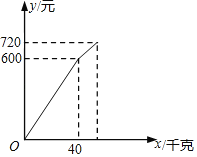
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=x2+bx–1的图象如图,对称轴为直线x=1,若关于x的一元二次方程x2–2x–1–t=0(t为实数)在–1<x<4的范围内有实数解,则t的取值范围是

A. t≥–2 B. –2≤t<7
C. –2≤t<2 D. 2<t<7
查看答案和解析>>
科目:初中数学 来源: 题型:
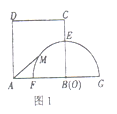
【题目】如图1,四边形![]() 是正方形,且
是正方形,且![]() ,点
,点![]() 与
与![]() 重合,以
重合,以![]() 为圆心,作半径长为5的半圆
为圆心,作半径长为5的半圆![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .
.
发现![]() 是半圆
是半圆![]() 上任意一点,连接
上任意一点,连接![]() ,则
,则![]() 的最大值为______;
的最大值为______;
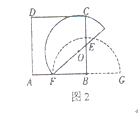
思考如图2,将半圆![]() 绕点
绕点![]() 逆时针旋转,记旋转角为
逆时针旋转,记旋转角为![]()
(1)当![]() 时,求半圆
时,求半圆![]() 落在正方形内部的弧长;
落在正方形内部的弧长;
(2)在旋转过程中,若半圆![]() 与正方形
与正方形![]() 的边相切时,请直接写出此时点
的边相切时,请直接写出此时点![]() 到切点的距离.(注:
到切点的距离.(注:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家推行“节能减排,低碳经济”政策后,低排量的汽车比较畅销,某汽车经销商购进A、B两种型号的低排量汽车,其中A型汽车的进货单价比B型汽车的进货单价多2万元;花50万元购进A型汽车的数量与花40万元购进B型汽车的数量相同.
(1)求A、B两种型号汽车的进货单价;
(2)销售中发现A型汽车的每周销量yA(台)与售价x(万元/台)满足函数关系yA=﹣x+20,B型汽车的每周销量yB(台)与售价x(万元/台)满足函数关系yB=﹣x+14,A型汽车的售价比B型汽车的售价高2万元/台.问A、B两种型号的汽车售价各为多少时,每周销售这两种汽车的总利润最大?最大利润是多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com