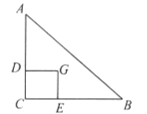
【题目】如图，在
中，
，过重心
作
、
的垂线，垂足分别为
、
，则四边形
的面积与的面积之比为（ ）
A.
B.
C.
D.
【答案】C
【解析】
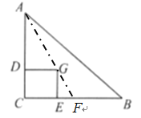
连接AG并延长交BC于点F，根据G为重心可知，AG=2FG，CF=BF，再证明△ADG∽△GEF，得出
，设矩形CDGE中，DG=a，EG=b，用含a,b的式子将AC，BC的长表示出来，再列式化简即可求出结果．
解：连接AG并延长交BC于点F，根据G为重心可知，AG=2FG，CF=BF，
易得四边形GDCE为矩形，
∴DG∥BC，DG=CD=EG=CE，∠CDG=∠CEG=90°，
∴∠AGD=∠AFC，∠ADG=∠GEF=90°，
∴△ADG∽△GEF，
∴
．
设矩形CDGE中，DG=a，EG=b，
∴AC=AD+CD=2EG+EG=3b，
BC=2CF=2(CE+EF)=2(DG+
)=3a，
∴
．
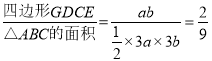故选：C．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：初中数学 来源： 题型：
【题目】某超市销售一种文具，进价为 5（元/件），售价为6（元/件）时，当天的销售量为100件，在销售过程中发现：售价每上涨0.5元，当天的销售量就减少5件，设当天销售单价统一为
（元/件）（
，且是按0.5元的倍数上涨），当天销售利润为
元．
（1）求与的函数关系式（不要求写出自变量的取值范围）；
（2）要使当天销售利润不低于240元，求当天销售单价的范围；
（3）若每件文具的利润不超过60%，要使当天获得利润最大，每件文具售价为多少元？并求出最大利润.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】知识背景：
当a＞0且x＞0时，因为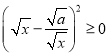
，所以x﹣2
≥0，从而
（当
，即x＝
时取等号）．
设函数y＝x+
（x＞0，a＞0），由上述结论可知：当x＝时，该函数有最小值2．
应用举例
已知函数为y1＝x（x＞0）与函数y2＝
（x＞0），则当x＝
时，y1+y2＝x+有最小值为2．
解决问题
（1）已知函数为y1＝x﹣1（x＞1）与函数y2＝（x﹣1）2+9（x＞1），当x取何值时，
有最小值？最小值是多少？
（2）已知某设备租赁使用成本包含以下三部分：一是设备的安装调试费用，共490元；二是设备的租赁使用费用，每天200元；三是设备的折旧费用，它与使用天数的平方成正比，比例系数为0．001．若设该设备的租赁使用天数为x天，则当x取何值时，该设备平均每天的租赁使用成本最低？最低是多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
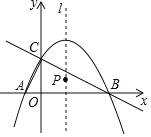
【题目】如图，已知抛物线y1＝﹣
x2+
x+2与x轴交于A、B两点，与y轴交于点C，直线l是抛物线的对称轴，一次函数y2＝kx+b经过B、C两点，连接AC．
（1）△ABC是 三角形；
（2）设点P是直线l上的一个动点，当△PAC的周长最小时，求点P的坐标；
（3）结合图象，写出满足y1＞y2时，x的取值范围 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
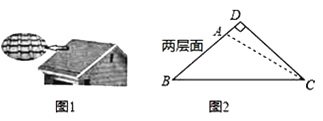
【题目】太阳能光伏建筑是现代绿色环保建筑之一，老张准备把自家屋顶改建成光伏瓦面，改建前屋顶截面△ABC如图2所示，BC=10米，∠ABC=∠ACB=36°，改建后顶点D在BA的延长线上，且∠BDC=90°，求改建后南屋面边沿增加部分AD的长．（结果精确到0.1米）
（参考数据：sin18°≈0.31，cos18°≈0.95．tan18°≈0.32，sin36°≈0.59．cos36°≈0.81，tan36°≈0.73）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图是由24个小正方形组成的网格图，每一个正方形的顶点都称为格点，
的三个顶点都是格点．请按要求完成下列作图，每个小题只需作出一个符合条件的图形．
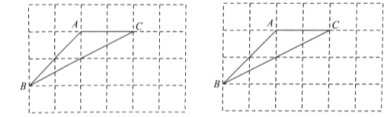
（1）在图1网格中找格点
，作直线
，使直线平分的面积；
（2）在图2网格中找格点
，作直线
，使直线把的面积分成
两部分．
查看答案和解析>>
科目：初中数学 来源： 题型：
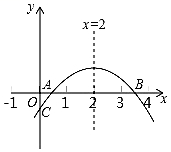
【题目】如图,二次函数
的图象与
轴正半轴相交于A、B两点,与
轴相交于点C,对称轴为直线
且OA=OC,则下列结论:①
②
③
④关于的方程
有一个根为
其中正确的结论个数有（ ）
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目：初中数学 来源： 题型：
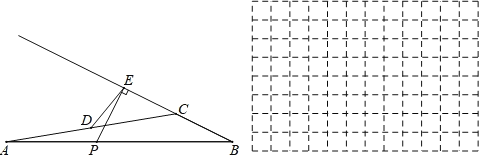
【题目】如图，在△ABC中，AB=4.4cm，点D是AC边的中点，点P是边AB上的一个动点，过点P作射线BC的垂线，垂足为点E，连接DE．设PA=xcm，ED=ycm，小石根据学习函数的经验，对函数y随自变量x的变化而变化的规律进行了探究．下面是小石的探究过程，请补充完整：
（1）通过取点、画图、测量，得到了x与y的几组值，如表：（说明：补全表格时相关数据保留一位小数）
（2）建立平面直角坐标系，描出已补全后的表中各对对应值为坐标的点，画出该函数的图象；
（3）结合画出的函数图象，解决问题：点E是BC边的中点时，PA的长度约为 cm．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，点O为坐标原点，过点O的抛物线y＝ax2﹣7ax与x轴正半轴交于点A，点D为第三象限抛物线上一点，AD交y轴于点B，OA＝2OB，点D纵坐标为﹣4．
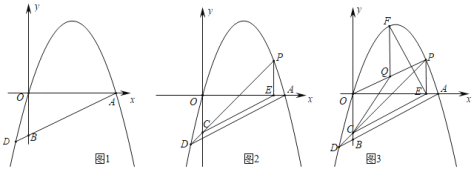
（1）如图1，求抛物线的解析式；
（2）如图2，点P为第一象限抛物线上一点，过点P作PE⊥x轴，垂足为E，PD交y轴于点C，连接CE，求证：CE∥AD；
（3）如图3，在（2）的条件下，将线段EC绕点E顺时针旋转90°，使点C恰好落在抛物线的点F处，连接OP，点Q为线段OP上一点，若∠FQC＝135°，求点Q坐标．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com