
【题目】如图,已知抛物线y1=﹣![]() x2+
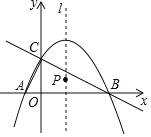
x2+![]() x+2与x轴交于A、B两点,与y轴交于点C,直线l是抛物线的对称轴,一次函数y2=kx+b经过B、C两点,连接AC.
x+2与x轴交于A、B两点,与y轴交于点C,直线l是抛物线的对称轴,一次函数y2=kx+b经过B、C两点,连接AC.
(1)△ABC是 三角形;
(2)设点P是直线l上的一个动点,当△PAC的周长最小时,求点P的坐标;
(3)结合图象,写出满足y1>y2时,x的取值范围 .
【答案】(1)直角;(2)P(![]() ,
,![]() );(3)0<x<4.
);(3)0<x<4.
【解析】
(1)求出点A、B、C的坐标分别为:(-1,0)、(4,0)、(0,2),则AB2=25,AC2=5,BC2=20,即可求解;
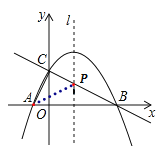
(2)点A关于函数对称轴的对称点为点B,则直线BC与对称轴的交点即为点P,即可求解;
(3)由图象可得:y1>y2时,x的取值范围为:0<x<4.
解:(1)当x=0时,
y1=0+0+2=2,
当y=0时,
﹣![]() x2+
x2+![]() x+2=0,
x+2=0,
解得
x1=-1,x2=4,
∴点A、B、C的坐标分别为:(﹣1,0)、(4,0)、(0,2),
则AB2=25,AC2=5,BC2=20,
故AB2=AC2+BC2,
故答案为:直角;
(2)将点B、C的坐标代入一次函数表达式:y=kx+b得:
![]() ,
,
解得
 ,
,
∴直线BC的表达式为:y=﹣![]() x+2,
x+2,
抛物线的对称轴为直线:x=![]() ,
,
点A关于函数对称轴的对称点为点B,则直线BC与对称轴的交点即为点P,
当x=![]() 时,y=
时,y=![]() ×
×![]() +2=
+2=![]() ,
,
故点P(![]() ,
,![]() );
);
(3)由图象可得:y1>y2时,x的取值范围为:0<x<4,
故答案为:0<x<4.


 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:
【题目】如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD,等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.
(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=x2+bx–1的图象如图,对称轴为直线x=1,若关于x的一元二次方程x2–2x–1–t=0(t为实数)在–1<x<4的范围内有实数解,则t的取值范围是

A. t≥–2 B. –2≤t<7
C. –2≤t<2 D. 2<t<7
查看答案和解析>>
科目:初中数学 来源: 题型:
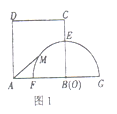
【题目】如图1,四边形![]() 是正方形,且
是正方形,且![]() ,点
,点![]() 与
与![]() 重合,以
重合,以![]() 为圆心,作半径长为5的半圆
为圆心,作半径长为5的半圆![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .
.
发现![]() 是半圆
是半圆![]() 上任意一点,连接
上任意一点,连接![]() ,则
,则![]() 的最大值为______;
的最大值为______;
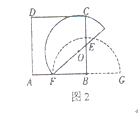
思考如图2,将半圆![]() 绕点
绕点![]() 逆时针旋转,记旋转角为
逆时针旋转,记旋转角为![]()
(1)当![]() 时,求半圆
时,求半圆![]() 落在正方形内部的弧长;
落在正方形内部的弧长;
(2)在旋转过程中,若半圆![]() 与正方形
与正方形![]() 的边相切时,请直接写出此时点
的边相切时,请直接写出此时点![]() 到切点的距离.(注:
到切点的距离.(注:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年5月,以“寻根国学,传承文明”为主题的兰州市第三届“国学少年强一国学知识挑战赛”总决赛拉开帷幕,小明晋级了总决赛.比赛过程分两个环节,参赛选手须在每个环节中各选择一道题目.
第一环节:写字注音、成语故事、国学常识、成语接龙(分别用![]() 表示);
表示);
第二环节:成语听写、诗词对句、经典通读(分别用![]() 表示)
表示)
(1)请用树状图或列表的方法表示小明参加总决赛抽取题目的所有可能结果
(2)求小明参加总决赛抽取题目都是成语题目(成语故事、成语接龙、成语听写)的概率。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四张背面完全相同的纸牌A、B、C、D,其中正面分别画有四个不同的几何图形(如图),小华将这4张纸牌背面朝上洗匀后摸出一张,放回洗匀后再摸一张.
(1)用树状图(或列表法)表示两次摸牌所有可能出现的结果(纸牌可用A、B、C、D表示);
(2)求摸出两张纸牌牌面上所画几何图形,既是轴对称图形又是中心对称图形的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ACB=90°,AC=4,AB=5,点E、F分别在AC、AB上,连接EF,将△ABC沿EF折叠,使点A落在BC边上的点D处.若△DEF有一边垂直BC,则EF=_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com