
【题目】如图,![]() 的直径
的直径![]() 垂直于弦
垂直于弦![]() ,垂足为
,垂足为![]() ,
,![]() 为
为![]() 延长线上一点,且
延长线上一点,且![]() .
.
(1)求证:![]() 为
为![]() 的切线;
的切线;
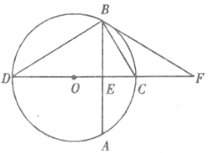
(2)若![]() ,
,![]() ,求
,求![]() 的半径.
的半径.
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2-2ax+c与x轴交于A,B两点,与y轴正半轴交于点C,且A(-1,0).
(1)一元二次方程ax2-2ax+c=0的解是 ;
(2)一元二次不等式ax2-2ax+c>0的解集是 ;
(3)若抛物线的顶点在直线y=2x上,求此抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学习小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如下折线统计图,则符合这一结果的实验最有可能的是( )

A. 袋中装有大小和质地都相同的3个红球和2个黄球,从中随机取一个,取到红球
B. 掷一枚质地均匀的正六面体骰子,向上的面的点数是偶数
C. 先后两次掷一枚质地均匀的硬币,两次都出现反面
D. 先后两次掷一枚质地均匀的正六面体骰子,两次向上的面的点数之和是7或超过9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中 AB = AC,点 D为 BC边的中点,点 F在边 AB上,点E在 线段 DF的延长线上,且∠BAE =∠BDF,点 M在线段 DF上,且∠EBM =∠C.
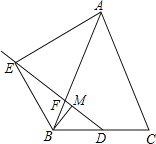
(1)求证: EB BD BM AB ;
(2)求证:AE⊥BE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.

(1)求证:△ABM∽△EFA;
(2)若AB=12,BM=5,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】北中环桥是省城太原的一座跨汾河大桥(如图1),它由五个高度不同,跨径也不同的抛物线型钢拱通过吊桥,拉锁与主梁相连,最高的钢拱如图2所示,此钢拱(近似看成二次函数的图象-抛物线)在同一竖直平面内,与拱脚所在的水平面相交于A,B两点,拱高为78米(即最高点O到AB的距离为78米),跨径为90米(即AB=90米),以最高点O为坐标原点,以平行于AB的直线为![]() 轴建立平面直角坐标系,则此抛物线钢拱的函数表达式为( )
轴建立平面直角坐标系,则此抛物线钢拱的函数表达式为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种文具,进价为 5(元/件),售价为6(元/件)时,当天的销售量为100件,在销售过程中发现:售价每上涨0.5元,当天的销售量就减少5件,设当天销售单价统一为![]() (元/件)(
(元/件)(![]() ,且
,且![]() 是按0.5元的倍数上涨),当天销售利润为
是按0.5元的倍数上涨),当天销售利润为![]() 元.
元.
(1)求![]() 与
与![]() 的函数关系式(不要求写出自变量的取值范围);
的函数关系式(不要求写出自变量的取值范围);
(2)要使当天销售利润不低于240元,求当天销售单价的范围;
(3)若每件文具的利润不超过60%,要使当天获得利润最大,每件文具售价为多少元?并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,边CD的中垂线交对角线BD于点E,交CD于点F,连结AE.若∠ABC=50°,则∠AEB的度数为( )
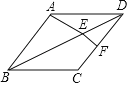
A.30°B.40°C.50°D.60°
查看答案和解析>>
科目:初中数学 来源: 题型:
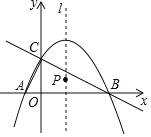
【题目】如图,已知抛物线y1=﹣![]() x2+
x2+![]() x+2与x轴交于A、B两点,与y轴交于点C,直线l是抛物线的对称轴,一次函数y2=kx+b经过B、C两点,连接AC.
x+2与x轴交于A、B两点,与y轴交于点C,直线l是抛物线的对称轴,一次函数y2=kx+b经过B、C两点,连接AC.
(1)△ABC是 三角形;
(2)设点P是直线l上的一个动点,当△PAC的周长最小时,求点P的坐标;
(3)结合图象,写出满足y1>y2时,x的取值范围 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com