
【题目】某超市销售一种文具,进价为 5(元/件),售价为6(元/件)时,当天的销售量为100件,在销售过程中发现:售价每上涨0.5元,当天的销售量就减少5件,设当天销售单价统一为![]() (元/件)(
(元/件)(![]() ,且
,且![]() 是按0.5元的倍数上涨),当天销售利润为
是按0.5元的倍数上涨),当天销售利润为![]() 元.
元.
(1)求![]() 与
与![]() 的函数关系式(不要求写出自变量的取值范围);
的函数关系式(不要求写出自变量的取值范围);
(2)要使当天销售利润不低于240元,求当天销售单价的范围;
(3)若每件文具的利润不超过60%,要使当天获得利润最大,每件文具售价为多少元?并求出最大利润.
【答案】(1)![]() ;(2)当天销售单价所在的范围为
;(2)当天销售单价所在的范围为![]() ;(3)每件文具售价为8元时,最大利润为240元.
;(3)每件文具售价为8元时,最大利润为240元.
【解析】
(1)根据当天销售利润等于每件利润乘以当天销量,找到当天销量与单价的关系即可得出答案;
(2)先求出利润等于240元时的单价,再根据二次函数图像的性质确定范围;
(3)先确定单价的范围,再根据二次函数的性质求最值.
(1)由题意![]()
∴![]() 与
与![]() 的函数关系式为:
的函数关系式为:![]()
(2)要使当天利润不低于240元,则![]() .
.
![]()
解得,![]() ,
,![]()
![]()
![]() ,抛物线的开口向下,
,抛物线的开口向下,
![]() 当天销售单价所在的范围为
当天销售单价所在的范围为![]()
(3)![]() 每件文具利润不超过60%
每件文具利润不超过60%
![]() ,得
,得![]()
![]() 文具的销售单价为
文具的销售单价为![]()
由(1)得![]()
![]() 对称轴为
对称轴为![]()
![]()
![]() 在对称轴的左侧,且
在对称轴的左侧,且![]() 随着
随着![]() 的增大而增大
的增大而增大
![]() 当
当![]() 时,取得最大值,此时
时,取得最大值,此时![]() ,
,
即每件文具售价为8元时,最大利润为240元.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】在某市的创优工作中,某社区计划对![]() 的区域进行绿化.经投标,由甲、乙两个施工队来完成,已知甲队每天能完成绿化面积是乙队每天能完成绿化面积的2倍,并且在独立完成面积为
的区域进行绿化.经投标,由甲、乙两个施工队来完成,已知甲队每天能完成绿化面积是乙队每天能完成绿化面积的2倍,并且在独立完成面积为![]() 区域的绿化时,甲队比乙队少用3天.
区域的绿化时,甲队比乙队少用3天.
(1)求甲、乙两施工队每天分别能完成的绿化面积是多少?
(2)设先由甲队施工m天,再由乙队施工n天,刚好完成绿化任务,
①求n与m的关系式;
②若甲、乙两队施工的总天数不超过14天,问甲工程队最少施工多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
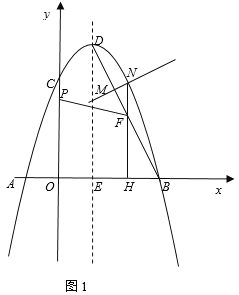
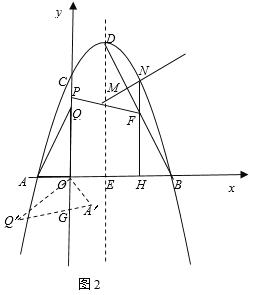
【题目】如图1,在平面直角坐标系中,抛物线y=ax2-2ax+3与x轴交于点A,B(点A在点B的左侧),交y轴于点C,点A的坐标为(-1,0),点D为抛物线的顶点,对称轴与x轴交于点E.
(1)填空:a= ,点B的坐标是 ;
(2)连结BD,点M是线段BD上一动点(点M不与端点B,D重合),过点M作MN⊥BD,交抛物线于点N(点N在对称轴的右侧),过点N作NH⊥x轴,垂足为H,交BD于点F,点P是线段OC上一动点,当△MNF的周长取得最大值时,求FP+![]() PC的最小值;
PC的最小值;
(3)在(2)中,当△MNF的周长取得最大值时,FP+![]() PC取得最小值时,如图2,把点P向下平移
PC取得最小值时,如图2,把点P向下平移![]() 个单位得到点Q,连结AQ,把△AOQ绕点O顺时针旋转一定的角度α(0°<α<360°),得到△A′OQ′,其中边A′Q′交坐标轴于点G.在旋转过程中,是否存在一点G,使得GQ′=OG?若存在,请直接写出所有满足条件的点Q′的坐标;若不存在,请说明理由.
个单位得到点Q,连结AQ,把△AOQ绕点O顺时针旋转一定的角度α(0°<α<360°),得到△A′OQ′,其中边A′Q′交坐标轴于点G.在旋转过程中,是否存在一点G,使得GQ′=OG?若存在,请直接写出所有满足条件的点Q′的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校就“遇见路人摔倒后如何处理”的问题,随机抽取该校部分学生进行问卷调查,图1和图2是整理数据后绘制的两幅不完整的统计图. 请根据图中提供的信息,解答下列问题:
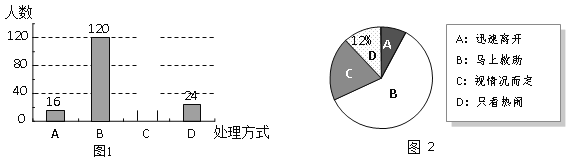
(1)该校随机抽查了 名学生?请将图1补充完整;
(2)在图2中,“视情况而定”部分所占的圆心角是 度;
(3)在这次调查中,甲、乙、丙、丁四名学生都选择“马上救助”,现准备从这四人中随机抽取两人进行座谈,试用列表或树形图的方法求抽取的两人恰好是甲和乙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织了2000名学生参加“爱我中华”知识竞赛活动,为了了解本次知识竞赛的成绩分布情况,从中抽取了部分学生的得分进行统计:
成绩 | 频数 | 频率 |
| 20 |
|
| 16 | 0.08 |
|
| 0.15 |
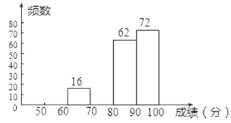
请你根据以上的信息,回答下列问题:
(1)![]() ,
,![]() ;
;
(2)在扇形统计图中,“成绩![]() 满足
满足![]() ”对应扇形的圆心角的度数是 ;
”对应扇形的圆心角的度数是 ;
(3)若将得分转化为等级,规定:![]() 评为
评为![]() ,
,![]() 评为
评为![]() ,
,![]() 评为
评为![]() ,
,![]() 评为
评为![]() .这次全校参加竞赛的学生约有 人参赛成绩被评为“
.这次全校参加竞赛的学生约有 人参赛成绩被评为“![]() ”.
”.
查看答案和解析>>
科目:初中数学 来源: 题型:
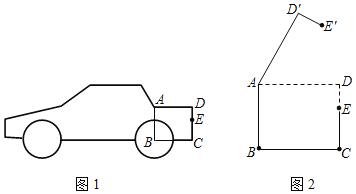
【题目】图1是某小型汽车的侧面示意图,其中矩形ABCD表示该车的后备箱,在打开后备箱的过程中,箱盖ADE可以绕点A逆时针方向旋转,当旋转角为60°时,箱盖ADE落在AD′E′的位置(如图2所示).已知AD=96厘米,DE=28厘米,EC=42厘米.
(1)求点D′到BC的距离;
(2)求E、E′两点的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
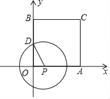
【题目】如图,正方形AOBC的顶点O在原点,边AO,BO分别在x轴和y轴上,点C坐标为(4,4),点D是BO的中点,点P是边OA上的一个动点,连接PD,以P为圆心,PD为半径作圆,设点P横坐标为t,当⊙P与正方形AOBC的边相切时,t的值为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com