
【题目】如图,已知AB是⊙O的直径,弦CD⊥AB于点E.点P是劣弧![]() 上任一点(不与点A,D重合),CP交AB于点M,AP与CD的延长相交于点F.
上任一点(不与点A,D重合),CP交AB于点M,AP与CD的延长相交于点F.

(1)设∠CPF=α,∠BDC=β,求证:α=β+90°;
(2)若OE=BE,设tan∠AFC=x,![]() .①求∠APC的度数;
.①求∠APC的度数;
②求y关于x的函数表达式及自变量x的取值范围.
【答案】(1)证明见解析;(2)①∠APC=60°;②y=![]() x,(0<x<
x,(0<x<![]() ).
).
【解析】
(1)CD⊥AB,则∠APC+∠CDB=90![]() ,即:180
,即:180![]() α+β=90
α+β=90![]() ,即可求解;
,即可求解;
(2)①证明△BOD为等边三角形,则∠CDB=30![]() ,即可求解;
,即可求解;
②在△CBM中,CH+HB=BC得:![]() ,
,![]() 得:
得:![]() ,即可求解.
,即可求解.
(1)∵CD⊥AB,
∴∠APC+∠CDB=90![]() ,即:180
,即:180![]() ﹣α+β=90
﹣α+β=90![]() ,
,
∴α=β+90![]() ;
;
(2)如图1,连接OD,
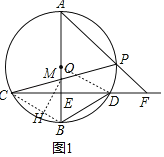
①OE=BE,OB⊥CD,设圆的半径为r,
∴∠BOD=∠OBD=∠ODB=60![]() ,
,
即:△BOD为等边三角形,
∴BC=r,
∴∠CDB=30![]() ,
,
∴∠APC=90![]() ﹣30
﹣30![]() =60
=60![]() ;
;
②连接BC,过点M组MH⊥BC于点H,
则∠MCB=∠FAB,∴∠CMH=∠F,
在△CBM中,设BC=r,∠CBA=60![]() ,
,
∴MH=BMsin∠CBA=![]() MB,
MB,
BH=![]() MB,CH=MHtan∠CMH=MHx,
MB,CH=MHtan∠CMH=MHx,
CH+HB=BC,即![]() ,
,
![]() ,而AM+BM=2r,
,而AM+BM=2r,
即:![]() ,
,
∴1![]() x=1+y,
x=1+y,
即:y=![]() x,(0<x
x,(0<x![]() ).
).


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线与![]() 轴交于点
轴交于点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,其对称轴
,其对称轴![]() 为
为![]() ,
,![]() 为抛物线上第二象限的一个动点.
为抛物线上第二象限的一个动点.
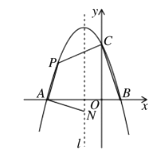
(1)求抛物线的解析式并写出其顶点坐标;
(2)当点![]() 在运动过程中,求四边形
在运动过程中,求四边形![]() 面积最大时的值及此时点
面积最大时的值及此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
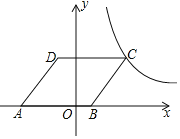
【题目】如图,在平面直角坐标系中,点O为坐标原点,菱形ABCD的顶点B在x轴的正半轴上,点A坐标为(-4,0),点D的坐标为(-1,4),反比例函数![]() 的图象恰好经过点C,则k的值为______.
的图象恰好经过点C,则k的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,AB为直径,点M为AB延长线上的一点,MC与⊙O相切于点C,圆周上有另一点D与点C分居直径AB两侧,且使得MC=MD=AC,连接AD.现有下列结论:①MD与⊙O相切;②四边形ACMD是菱形;③AB=MO;④∠ADM=120°,其中正确的结论有( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
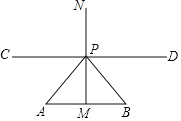
【题目】如图,线段AB=a,点P是AB中垂线MN上的一动点,过点P作直线CD∥AB.若在直线CD上存在点Q使得△ABQ为等腰三角形,且满足条件的点Q有且只有3个,则PM的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD,等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.
(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小卖部从批发市场购进一批李子,在销售了部分李子之后,余下的每千克降价3元,直至全部售完.销售金额(元)与李子销售量(千克)之间的关系如图所示.若销售这批李子一共赢利220元,那么这批李子的进价是_____元.
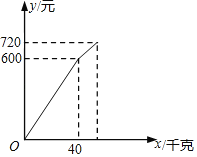
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,四边形![]() 是正方形,且
是正方形,且![]() ,点
,点![]() 与
与![]() 重合,以
重合,以![]() 为圆心,作半径长为5的半圆
为圆心,作半径长为5的半圆![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .
.
发现![]() 是半圆
是半圆![]() 上任意一点,连接
上任意一点,连接![]() ,则
,则![]() 的最大值为______;
的最大值为______;
思考如图2,将半圆![]() 绕点
绕点![]() 逆时针旋转,记旋转角为
逆时针旋转,记旋转角为![]()
(1)当![]() 时,求半圆
时,求半圆![]() 落在正方形内部的弧长;
落在正方形内部的弧长;
(2)在旋转过程中,若半圆![]() 与正方形
与正方形![]() 的边相切时,请直接写出此时点
的边相切时,请直接写出此时点![]() 到切点的距离.(注:
到切点的距离.(注:![]() ,
,![]() ,
,![]() )
)
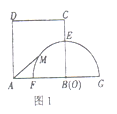
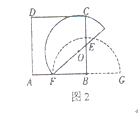
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下是通过折叠正方形纸片得到等边三角形的步骤取一张正方形的纸片进行折叠,具体操作过程如下:
第一步:如图,先把正方形ABCD对折,折痕为MN;
第二步:点E在线段MD上,将△ECD沿EC翻折,点D恰好落在MN上,记为点P,连接BP可得△BCP是等边三角形
问题:在折叠过程中,可以得到PB=PC;依据是________________________.
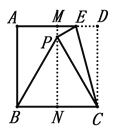
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com