
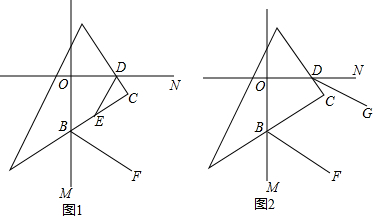
分析 (1)先利用垂直定义得到∠MON=90°,然后利用四边形内角和求解;
(2)延长DE交BF于H,如图,由于∠OBC+∠ODC=180°,∠OBC+∠CBM=180°,根据等角的补角相等得到∠ODC=∠CBM,由于DE平分∠ODC,BF平分∠CBM,则∠CDE=∠FBE,然后根据三角形内角和可得∠BHE=∠C=90°,于是DE⊥BF;
(3)作CQ∥BF,如图2,由于∠OBC+∠ODC=180°,则∠CBM+∠NDC=180°,再利用BF、DG分别平分∠OBC、∠ODC的外角,则∠GDC+∠FBC=90°,根据平行线的性质,由CQ∥BF得∠FBC=∠BCQ,加上∠BCQ+∠DCQ=90°,则∠DCQ=∠GDC,于是可判断CQ∥GD,所以BF∥DG.
解答 (1)解:∵OM⊥ON,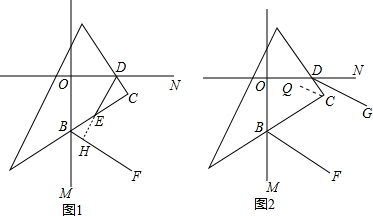
∴∠MON=90°,
在四边形OBCD中,∠C=∠BOD=90°,
∴∠OBC+∠ODC=360°-90°-90°=180°;
故答案为180°;
(2)证明:延长DE交BF于H,如图1,
∵∠OBC+∠ODC=180°,
而∠OBC+∠CBM=180°,
∴∠ODC=∠CBM,
∵DE平分∠ODC,BF平分∠CBM,
∴∠CDE=∠FBE,
而∠DEC=∠BEH,
∴∠BHE=∠C=90°,
∴DE⊥BF;
(3)解:DG∥BF.理由如下:
作CQ∥BF,如图2,
∵∠OBC+∠ODC=180°,
∴∠CBM+∠NDC=180°,
∵BF、DG分别平分∠OBC、∠ODC的外角,
∴∠GDC+∠FBC=90°,
∵CQ∥BF,
∴∠FBC=∠BCQ,
而∠BCQ+∠DCQ=90°,
∴∠DCQ=∠GDC,
∴CQ∥GD,
∴BF∥DG.
点评 本题考查了垂线的定义:当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线,它们的交点叫做垂足.也考查了平行线的判定与性质.


科目:初中数学 来源: 题型:选择题
| A. | 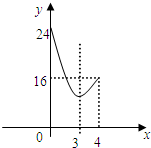 | B. | 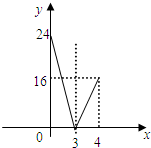 | ||
| C. | 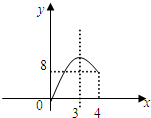 | D. | 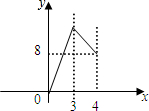 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
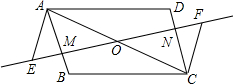 如图,O为?ABCD的对角线AC的中点,过点O的一条直线分别与AB、CD交于点M、N,点E、F在直线MN上,且OE=OF.
如图,O为?ABCD的对角线AC的中点,过点O的一条直线分别与AB、CD交于点M、N,点E、F在直线MN上,且OE=OF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.15×10-9 | B. | 1.5×10-10 | C. | 1.5×10-9 | D. | 0.15×10-10 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
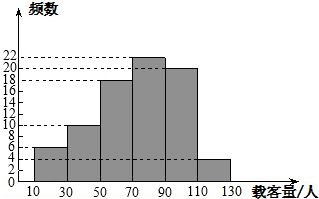 为了解我市3路公共汽车的运营情况,公交部门随机统计了某天3路公共汽车每个运行班次的载客量,得到如下频数分布直方图.如果以各组的组中值代表各组实际数据,请分析统计数据完成下列问题.(注:一个小组的组中值是指这个小组的两个端点数的平均数)
为了解我市3路公共汽车的运营情况,公交部门随机统计了某天3路公共汽车每个运行班次的载客量,得到如下频数分布直方图.如果以各组的组中值代表各组实际数据,请分析统计数据完成下列问题.(注:一个小组的组中值是指这个小组的两个端点数的平均数)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
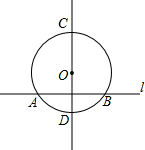 如图,已知⊙O的半径为5cm,直线CD经过圆心O,直线l与直线CD垂直,交⊙O于A、B两点,且AB=8cm.如果直线l与⊙O相切,那么直线l应平移2cm或8cm.
如图,已知⊙O的半径为5cm,直线CD经过圆心O,直线l与直线CD垂直,交⊙O于A、B两点,且AB=8cm.如果直线l与⊙O相切,那么直线l应平移2cm或8cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com