
【题目】川西某高原上有一条笔直的公路,在紧靠公路相距40千米的A、B两地,分别有甲、乙两个医疗站,如图,在A地北偏东45°,B地北偏西60°方向上有一牧民区C,过点C作CH⊥AB于H.
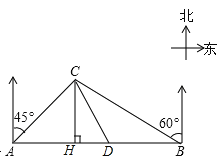
(1)求牧民区C到B地的距离(结果用根式表示);
(2)一天,乙医疗队的医生要到牧民区C出诊,她先由B地搭车沿公路AB到D处(BD<HB)转车,再由D地沿DC方向到牧民区C.若C、D两地距离是B、C两地距离的![]() 倍,求∠ADC的度数及B、D两地的距离(结果保留根号).
倍,求∠ADC的度数及B、D两地的距离(结果保留根号).
【答案】(1) 牧民区C到B地的距离为(40![]() -40)千米;(2) BD之间的距离为4.7千米.
-40)千米;(2) BD之间的距离为4.7千米.
【解析】
试题解析:(1)设CH为未知数,分别表示出AH,BH的值,让其相加得40求值即可求得CH的长,进而可求得CB的长;
(2)由CD和BC的数量关系可得CD和CH的数量关系,进而可得HD的长,让BH的长减去DH的长即为BD的距离.
试题解析:(1)设CH为x千米,由题意得,∠CBH=30°,∠CAH=45°,
∴AH=CH=x,
在Rt△BCH中,tan30°=![]() ,
,
∴BH=![]() x,
x,
∵AH+HB=AB=40,
∴x+![]() x=40,
x=40,
解得x=20![]() -20,
-20,
∴CB=2CH=40![]() -40.
-40.
答:牧民区C到B地的距离为(40![]() -40)千米;
-40)千米;
(2)∵C、D 两地距离是B、C两地距离的![]() 倍,CH=
倍,CH=![]() BC,
BC,
∴DC=![]() (40
(40![]() -40)=60-20
-40)=60-20![]() ,BH=
,BH=![]() x=
x=![]() (20
(20![]() -20)=60-20
-20)=60-20![]() ,
,
∴DH=![]() CH=20
CH=20![]() -20
-20![]() ,
,
∴BD=BH-DH=(60-20![]() )-(20
)-(20![]() -20
-20![]() )=60-20
)=60-20![]() -20
-20![]() +20
+20![]() ≈4.7.
≈4.7.
答:BD之间的距离为4.7千米.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,点E是BC边的中点,连接AE并延长与DC的延长线交于F.
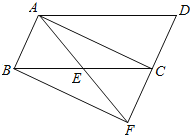
(1)求证:CF=CD;
(2)若AF平分∠BAD,连接DE,试判断DE与AF的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一副三角板如图甲放置,其中∠ACB=DEC=90°,∠A=45°,∠D=30°,AB=6cm,DC=7cm.把三角板DCE绕点C顺时针旋转15°得到△D′CE′,如图乙,这时AB与CD′相交于点O,D′E′与AB、CB分别相交于点F、G,连接AD′.

(1)求∠OFE′的度数;
(2)求线段AD′的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当x=3时,代数式px3+qx+1的值为2002,则当x=-3时,代数式px3+qx+1的值为( )
A. 2000 B. -2002 C. -2000 D. 2001
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com