
【题目】如图,在矩形纸片ABCD中,已知AB=1,BC= ![]() ,点E在边CD上移动,连接AE,将多边形ABCE沿直线AE翻折,得到多边形AB′C′E,点B、C的对应点分别为点B′、C′.
,点E在边CD上移动,连接AE,将多边形ABCE沿直线AE翻折,得到多边形AB′C′E,点B、C的对应点分别为点B′、C′.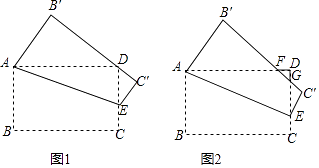
(1)当B′C′恰好经过点D时(如图1),求线段CE的长;
(2)若B′C′分别交边AD,CD于点F,G,且∠DAE=22.5°(如图2),求△DFG的面积;
(3)在点E从点C移动到点D的过程中,求点C′运动的路径长.
【答案】
(1)
解:如图1中,设CE=EC′=x,则DE=1﹣x,
∵∠ADB′+∠EDC′=90°,∠B′AD+∠ADB′=90°,
∴∠B′AD=∠EDC′,
∵∠B′=∠C′=90°,AB′=AB=1,AD= ![]() ,
,
∴DB′= ![]() =
= ![]() ,
,
∴△ADB′′∽△DEC,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴x= ![]() ﹣2.
﹣2.
∴CE= ![]() ﹣2.
﹣2.
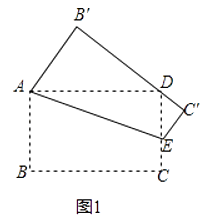
(2)
解:如图2中,
∵∠BAD=∠B′=∠D=90°,∠DAE=22.5°,
∴∠EAB=∠EAB′=67.5°,
∴∠B′AF=∠B′FA=45°,
∴∠DFG=∠AFB′=∠DGF=45°,
∴DF=FG,
在Rt△AB′F中,AB′=FB′=1,
∴AF= ![]() AB′=
AB′= ![]() ,
,
∴DF=DG= ![]() ﹣
﹣ ![]() ,
,
∴S△DFG= ![]() (
( ![]() ﹣
﹣ ![]() )2=
)2= ![]() ﹣
﹣ ![]()

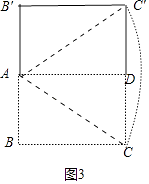
(3)
解:如图3中,点C的运动路径的长为 ![]() 的长,
的长,
在Rt△ADC中,∵tan∠DAC= ![]() =
= ![]() ,
,
∴∠DAC=30°,AC=2CD=2,
∵∠C′AD=∠DAC=30°,
∴∠CAC′=60°,
∴ ![]() 的长=
的长= ![]() =
= ![]() π.
π.
【解析】(1)如图1中,设CE=EC′=x,则DE=1﹣x,由△ADB′′∽△DEC,可得 ![]() =
= ![]() ,列出方程即可解决问题;(2)如图2中,首先证明△ADB′,△DFG都是等腰直角三角形,求出DF即可解决问题;(3)如图3中,点C的运动路径的长为
,列出方程即可解决问题;(2)如图2中,首先证明△ADB′,△DFG都是等腰直角三角形,求出DF即可解决问题;(3)如图3中,点C的运动路径的长为 ![]() 的长,求出圆心角、半径即可解决问题.
的长,求出圆心角、半径即可解决问题.
【考点精析】根据题目的已知条件,利用等腰直角三角形和圆心角、弧、弦的关系的相关知识可以得到问题的答案,需要掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等;在同圆或等圆中,同弧等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.


科目:初中数学 来源: 题型:
【题目】某乡镇企业生产部有技术工人15人,生产部为了合理制定产品的每月生产定额,统计了15人某月的加工零件个数:
加工件数 | 540 | 450 | 300 | 240 | 210 | 120 |
人数 | 1 | 1 | 2 | 6 | 3 | 2 |
(1)写出这15人该月加工零件数的平均数、中位数和众数.
(2)假如生产部负责人把每位工人的月加工零件数定为260(件),你认为这个定额是否合理,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,现有甲、乙两个小分队分别同时从B、C两地出发前往A地,甲沿线路BA行进,乙沿线路CA行进,已知C在A的南偏东55°方向,AB的坡度为1:5,同时由于地震原因造成BC路段泥石堵塞,在BC路段中位于A的正南方向上有一清障处H,负责抢修BC路段,已知BH为12000m.
(1)求BC的长度;
(2)如果两个分队在前往A地时匀速前行,且甲的速度是乙的速度的三倍.试判断哪个分队先到达A地.(tan55°≈1.4,sin55°≈0.84,cos55°≈0.6, ![]() ≈5.01,结果保留整数)
≈5.01,结果保留整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了测得一棵树的高度AB,小明在D处用高为1m的测角仪CD,测得树顶A的仰角为45°,再向树方向前进10m,又测得树顶A的仰角为60°,求这棵树的高度AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】桌面上有四张正面分别标有数字1,2,3,4的不透明卡片,它们除数字外其余全部相同,现将它们背面朝上洗匀.
(1)随机翻开一张卡片,正面所标数字大于2的概率为;
(2)随机翻开一张卡片,从余下的三张卡片中再翻开一张,求翻开的两张卡片正面所标数字之和是偶数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组  请结合题意,完成本题的解答.
请结合题意,完成本题的解答.
(1)解不等式①,得 , 依据是: .
(2)解不等式③,得 .
(3)把不等式①,②和③的解集在数轴上表示出来. ![]()
(4)从图中可以找出三个不等式解集的公共部分,得不等式组的解集 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】折纸的思考.
用一张矩形纸片折等边三角形.
第一步,对折矩形纸片ABCD(AB>BC)(图①),使AB与DC重合,得到折痕EF,把纸片展平(图②).
第二步,如图③,再一次折叠纸片,使点C落在EF上的P处,并使折痕经过点B,得到折痕BG,折出PB,PC,得到△PBC.
(1)说明△PBC是等边三角形.
(2)如图④,小明画出了图③的矩形ABCD和等边三角形PBC,他发现,在矩形ABCD中把△PBC经过图形变化,可以得到图⑤中的更大的等边三角形,请描述图形变化的过程.
(3)已知矩形一边长为3cm,另一边长为a cm,对于每一个确定的a的值,在矩形中都能画出最大的等边三角形,请画出不同情形的示意图,并写出对应的a的取值范围.
(4)用一张正方形铁片剪一个直角边长分别为4cm和1cm的直角三角形铁片,求所需正方形铁片的边长的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在边长为1的小正方形组成的方格纸中,若多边形的各顶点都在方格纸的格点(横竖格子线的交错点)上,这样的多边形称为格点多边形.记格点多边形内的格点数为a,边界上的格点数为b,则格点多边形的面积可表示为S=ma+nb﹣1,其中m,n为常数.
(1)在下面的方格中各画出一个面积为6的格点多边形,依次为三角形、平行四边形(非菱形)、菱形;
(2)利用(1)中的格点多边形确定m,n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】方成同学看到一则材料:甲开汽车,乙骑自行车从M地出发沿一条公路匀速前往N地.设乙行驶的时间为t(h),甲乙两人之间的距离为y(km),y与t的函数关系如图1所示. 方成思考后发现了如图1的部分正确信息:乙先出发1h;甲出发0.5小时与乙相遇.
请你帮助方成同学解决以下问题: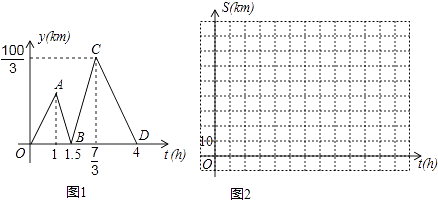
(1)分别求出线段BC,CD所在直线的函数表达式;
(2)当20<y<30时,求t的取值范围;
(3)分别求出甲,乙行驶的路程S甲 , S乙与时间t的函数表达式,并在图2所给的直角坐标系中分别画出它们的图象;
(4)丙骑摩托车与乙同时出发,从N地沿同一公路匀速前往M地,若丙经过 ![]() h与乙相遇,问丙出发后多少时间与甲相遇?
h与乙相遇,问丙出发后多少时间与甲相遇?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com