
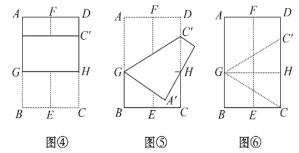
【题目】如图,将矩形纸片ABCD按如下顺序折叠:对折、展平,得折痕EF(如图①);沿GC折叠,使点B落在EF上的点B′处(如图②);展平,得折痕GC(如图③),沿GH折叠,使点C落在DH上的C′处(如图④);沿GC′折叠(如图⑤);展平,得折痕GC′,GH(如图⑥).
(1)求图②中∠BCB′=______度;
(2)图⑥中的△GCC′是_______三角形.

【答案】60, 等边
【解析】
(1)由折叠的性质知:B′C=BC,然后在Rt△B′EC中,含30°角的直角三角形的性质,即可求得∠BCB′的度数;
(2)首先根据题意得:GC平分∠BCB′,即可求得∠GCC′的度数,然后由折叠的性质知:GH是线段CC′的对称轴,可得GC′=GC,即可得△GCC′是等边三角形.
(1)由折叠的性质知:B′C=BC.在Rt△B′EC中,∵EC是斜边B′C的一半,∴∠EB′C=30°,∴∠BCB′=60°,即∠BCB′=60°;
(2)图⑥中的△CGC'是等边三角形.理由如下:
∵GC平分∠BCB′,∴∠GCB=![]() ∠GCC′=
∠GCC′=![]() ∠BCB′=30°,∴∠GCC′=∠BCD﹣∠BCG=60°,由折叠的性质知:GH是线段CC′的对称轴,∴GC′=GC,∴△GCC′是等边三角形.
∠BCB′=30°,∴∠GCC′=∠BCD﹣∠BCG=60°,由折叠的性质知:GH是线段CC′的对称轴,∴GC′=GC,∴△GCC′是等边三角形.


 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:初中数学 来源: 题型:
【题目】如图,⊙O为△ABC的外接圆,直线l与⊙O相切与点P,且l∥BC. 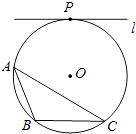
(1)请仅用无刻度的直尺,在⊙O中画出一条弦,使这条弦将△ABC分成面积相等的两部分(保留作图痕迹,不写作法);
(2)请写出证明△ABC被所作弦分成的两部分面积相等的思路.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如表:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | 0 | 4 | 6 | 6 | 4 | … |
从表可知,
①抛物线与x轴的交点为;
②抛物线的对称轴是;
③函数y=ax2+bx+c的最大值为;
④x , y随x增大而增大.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,D是BA延长线上一点,AE是∠DAC的平分线,P是AE上的一点(点P不与点A重合),连接PB,PC.通过观察,测量,猜想PB+PC与AB+AC之间的大小关系,并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠A=36°,BD、CE分别是∠ABC、∠BCD的角平分线,则图中的等腰三角形有( )

A. 5个 B. 4个 C. 3个 D. 2个
查看答案和解析>>
科目:初中数学 来源: 题型:
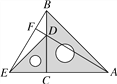
【题目】把两个含有45°角的直角三角板ACB和DEC如图放置,点A,C,E在同一直线上,点D在BC上,连接BE,AD,AD的延长线交BE于点F.
(1)求证:△ADC≌△BEC;
(2)猜想AD与EB是否垂直?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,D是BC的中点,过D点的直线GF交AC于F,交AC的平行线BG于G点,DE⊥DF,交AB于点E,连结EG、EF.

(1)求证:BG=CF.
(2)请你判断BE+CF与EF的大小关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果关于x的不等式组 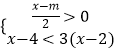 的解集为x>1,且关于x的分式方程
的解集为x>1,且关于x的分式方程 ![]() +
+ ![]() =3有非负整数解,则符合条件的m的所有值的和是( )
=3有非负整数解,则符合条件的m的所有值的和是( )
A.﹣2
B.﹣4
C.﹣7
D.﹣8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 、
、![]() 、
、![]() 在数轴上的位置如图所示,所对应的点分别为
在数轴上的位置如图所示,所对应的点分别为![]() 、
、![]() 、
、![]() ,
,
![]()
![]() 在数轴上表示
在数轴上表示![]() 的点与表示
的点与表示![]() 的点之间的距离为________;
的点之间的距离为________;
在数轴上表示![]() 的点与表示
的点与表示![]() 的点之间的距离为________;
的点之间的距离为________;
在数轴上表示![]() 的点与表示
的点与表示![]() 的点之间的距离为________;
的点之间的距离为________;
由此可得点![]() 、
、![]() 之间的距离为________,点
之间的距离为________,点![]() 、
、![]() 之间的距离为________,点
之间的距离为________,点![]() 、
、![]() 之间的距离为________
之间的距离为________
![]() 化简:
化简:![]() ;
;
![]() 若
若![]() ,
,![]() 的倒数是它本身,
的倒数是它本身,![]() 的绝对值的相反数是
的绝对值的相反数是![]() ,
,
求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com