Question

【题目】在Rt△ABC中，∠BAC=90°，D是BC的中点，E是AD的中点，过点A作AF∥BC交BE的延长线于点F．

（1）求证：△AEF≌△DEB；

（2）证明四边形ADCF是菱形；

（3）若AC=3，AB=4，求菱形ADCF的面积．

Answer 1

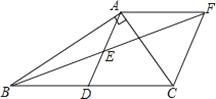
【答案】（1）证明见解析；（2）证明见解析；（3）菱形ADCF的面积为6．

【解析】试题分析: （1）根据AAS证△AFE≌△DBE；

（2）利用全等三角形的对应边相等得到AF=BD．证出四边形ADCF是平行四边形，再由“直角三角形斜边的中线等于斜边的一半”得到AD=DC，从而得出结论；

（3）由直角三角形ABC与菱形有相同的高，根据等积变形求出这个高，代入菱形面积公式可求出结论．

试题解析:

（1）证明：①∵AF∥BC，

∴∠AFE=∠DBE，

∵E是AD的中点，AD是BC边上的中线，

∴AE=DE，BD=CD，

在△AFE和△DBE中，

，

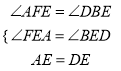∴△AFE≌△DBE（AAS）；

（2）证明：由（1）知，△AFE≌△DBE，则AF=DB．

∵DB=DC，

∴AF=CD．

∵AF∥BC，

∴四边形ADCF是平行四边形，

∵∠BAC=90°，D是BC的中点，E是AD的中点，

∴AD=DC=BC，

∴四边形ADCF是菱形；.

（3）连接DF，

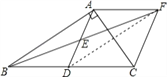
∵AF∥BD，AF=BD，

∴四边形ABDF是平行四边形，

∴DF=AB=4，

∵四边形ADCF是菱形，

∴S菱形ADCF=ACDF=×3×4=6．