
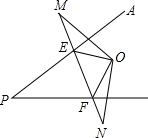
 如图所示,已知O是∠APB内的一点,点M、N分别是O点关于PA、PB的对称点,MN与PA、PB分别相交于点E、F,已知MN=5cm.
如图所示,已知O是∠APB内的一点,点M、N分别是O点关于PA、PB的对称点,MN与PA、PB分别相交于点E、F,已知MN=5cm.分析 (1)根据轴对称的性质,可得MW与OM的关系,OF与FN的关系,根据三角形的周长公式,可得答案;
(2)根据轴对称的性质,可得PM与PO的关系,PO与PN的关系,根据等腰三角形的判定,可得答案;
(3)根据轴对称的性质,可得∠MPA与∠APO的关系,∠OPB与∠BPN的关系,根据角的和查,可得答案.
解答 解:(1)由点M、N分别是O点关于PA、PB的对称点,得
ME=EO,FN=FO.
由三角形的周长,得
C△OEF=OE+EF+OF=ME+EF+FN=MN=5cm;
(2)如图: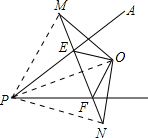 ,
,
由点M、N分别是O点关于PA、PB的对称点,得
PM=PO,PO=PN,
PM=PN,
△PMN是等腰三角形;
(3)由点M、N分别是O点关于PA、PB的对称点,得
∠APO=∠APM,∠BPO=∠BPN.
由角的和差,得
∠APO+∠BPO=∠APB=α,
∠APM+∠BPN=∠APO+∠BPO=∠APB=α,
∠MPN=∠MPA+∠APO+∠BPO+∠BPN=α+α=2α.
点评 本题考查了轴对称,利用对称轴上的点到线段两端点的距离相等是解题关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 如图,是用硬纸板做成的两个小直角三角形和一个大直角三角形,两个小直角三角形直角边长分别为a和b,斜边为c,大直角三角形直角边都为c,请你动动脑筋,将它们拼成一个能证明勾股定理的图形,并用这个图形证明勾股定理.
如图,是用硬纸板做成的两个小直角三角形和一个大直角三角形,两个小直角三角形直角边长分别为a和b,斜边为c,大直角三角形直角边都为c,请你动动脑筋,将它们拼成一个能证明勾股定理的图形,并用这个图形证明勾股定理.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 小萍要在一幅长60cm、宽40cm的风景画的四周外围,镶上一条宽度相同的金色纸边,制成一幅挂画(如图),使风景画的面积是整幅挂图面积54%.设金色纸边的宽为xcm,根据题意所列方程为( )
小萍要在一幅长60cm、宽40cm的风景画的四周外围,镶上一条宽度相同的金色纸边,制成一幅挂画(如图),使风景画的面积是整幅挂图面积54%.设金色纸边的宽为xcm,根据题意所列方程为( )| A. | (60+x)(40+x)×54%=60×40 | B. | (60+2x)(40+2x)×54%=60×40 | ||
| C. | (60+2x)(40+2x)=60×40×54% | D. | (60+x)(40+x)=60×40×54% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| n | 60° | 72° | 90° | 120° |
| R关于r的函数解析式 | 6r | 5r | 4r | 3r |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com