
【题目】如图,已知抛物线y=﹣x2+bx+c经过A(0,1)、B(4,3)两点.

(1)求抛物线的解析式;
(2)求tan∠ABO的值;
(3)过点B作BC⊥x轴,垂足为C,点M是抛物线上的一个动点,直线MN平行于y轴交直线AB于N,如果M、N、B、C为顶点的四边形是平行四边形,请直接写出M点的横坐标;
(4)已知点E为抛物线上位于第二象限内任一点,且E点横坐标为m,作边长为10的正方形EFGH,使EF∥x轴,点G在点E的右上方,那么,对于大于或等于﹣1的任意实数m,FG边与过A、B两点的直线都有交点,请说明理由.
【答案】(1)y=﹣x2+![]() +1;(2)
+1;(2)![]() (3)m=1或3或2+
(3)m=1或3或2+![]() 或2﹣
或2﹣![]() .(4)对于大于或等于﹣1的任意实数m,FG边与过A、B两点的直线都有交点,理由见解析
.(4)对于大于或等于﹣1的任意实数m,FG边与过A、B两点的直线都有交点,理由见解析
【解析】
试题分析:(1)把A、B两点坐标代入解析式即可解决.
(2)如图作AM⊥OB垂足为M,利用tan∠ABO=![]() 解决.
解决.
(3)根据MN=BC,列出方程即可解决.
(4)如图只要判断Gy>Ny即可.
解:(1)由题意![]() ,解得
,解得![]() ,所以抛物线解析式为y=﹣x2+
,所以抛物线解析式为y=﹣x2+![]() +1.
+1.
(2)如图作AM⊥OB垂足为M,∵直线AB的解析式为y=![]() x+1,直线OB的解析式为y=
x+1,直线OB的解析式为y=![]() x,
x,
∴直线AM为y=﹣2x+1,
由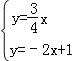 解得
解得![]() ,
,
∴直线点M坐标(![]() ,
,![]() )
)
∴AM=![]() BM=
BM=![]()
∴tan∠ABO=![]() =
=![]() .
.
(3)设点M坐标为(m,﹣m2+![]() m+1),当MN∥BC,MN=BC时,M、N、B、C为顶点的四边形是平行四边形,
m+1),当MN∥BC,MN=BC时,M、N、B、C为顶点的四边形是平行四边形,
∴|﹣m2+![]() m+1﹣(
m+1﹣(![]() m+1)|=3,
m+1)|=3,
整理得m2﹣4m+3=0或m2﹣4m﹣3=0,
解得m=1或3或2+![]() 或2﹣
或2﹣![]() .
.
(4)如图设FG与直线AB交于点N,
∵点E的横坐标为m,且点E在第二象限,﹣1<m<0,
又∵正方形EFGH的边长为10,
∴点F的横坐标为a,9<a<10,
∵直线AB的解析式为y=![]() x+1,
x+1,
∴点N的纵坐标![]() <Ny<6,
<Ny<6,
∵点G的纵坐标11<Gy<10,
∴Gy>Ny,
∴对于大于或等于﹣1的任意实数m,FG边与过A、B两点的直线都有交点.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,已知第一象限内的图象是反比例函数y=![]() 图象的一个分支,第二象限内的图象是反比例函数y=﹣
图象的一个分支,第二象限内的图象是反比例函数y=﹣![]() 图象的一个分支,在x轴的上方有一条平行于x轴的直线l与它们分别交于点A、B,过点A、B作x轴的垂线,垂足分别为C、D.若四边形ABCD的周长为8且AB<AC,则点A的坐标为 .
图象的一个分支,在x轴的上方有一条平行于x轴的直线l与它们分别交于点A、B,过点A、B作x轴的垂线,垂足分别为C、D.若四边形ABCD的周长为8且AB<AC,则点A的坐标为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M,N.
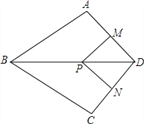
(1)求证:∠ADB=∠CDB;
(2)若∠ADC=90°,求证:四边形MPND是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,AB是⊙O的直径,AE是弦,C是劣弧AE的中点,过C作CD⊥AB于点D,CD交AE于点F,过C作CG∥AE交BA的延长线于点G.

(1)求证:CG是⊙O的切线.
(2)求证:AF=CF.
(3)若∠EAB=30°,CF=2,求GA的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设地面气温为20℃,如果每升高1千米,气温下降6℃,在这个变化过程中,自变量是________,因变量是________,如果高度用h(千米)表示,气温用t(℃)表示,那么t随h的变化而变化的关系式为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com