
【题目】如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M,N.
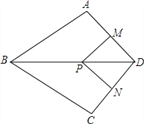
(1)求证:∠ADB=∠CDB;
(2)若∠ADC=90°,求证:四边形MPND是正方形.
【答案】(1)(2)证明见解析
【解析】试题分析:(1)根据角平分线的性质和全等三角形的判定方法证明△ABD≌△CBD,由全等三角形的性质即可得到:∠ADB=∠CDB;
(2)若∠ADC=90°,由(1)中的条件可得四边形MPND是矩形,再根据两边相等的四边形是正方形即可证明四边形MPND是正方形.
证明:(1)∵对角线BD平分∠ABC,
∴∠ABD=∠CBD,
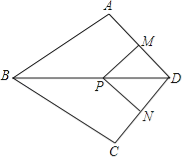
在△ABD和△CBD中,
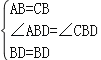 ,
,
∴△ABD≌△CBD(SAS),
∴∠ADB=∠CDB;
(2)∵PM⊥AD,PN⊥CD,
∴∠PMD=∠PND=90°,
∵∠ADC=90°,
∴四边形MPND是矩形,
∵∠ADB=∠CDB,
∴∠ADB=45°
∴PM=MD,
∴四边形MPND是正方形.


科目:初中数学 来源: 题型:
【题目】气象台预报“本市明天降水概率是30%”,对此消息下列说法正确的是( )
A.本市明天将有30%的地区降水
B.本市明天将有30%的时间降水
C.本市明天有可能降水
D.本市明天肯定不降水
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=﹣mx2+4x+2m与x轴交于点A(α,0),B(β,0),且![]() =﹣2,
=﹣2,

(1)求抛物线的解析式.
(2)抛物线的对称轴为l,与y轴的交点为C,顶点为D,点C关于l的对称点为E,是否存在x轴上的点M,y轴上的点N,使四边形DNME的周长最小?若存在,请画出图形(保留作图痕迹),并求出周长的最小值;若不存在,请说明理由.
(3)若点P在抛物线上,点Q在x轴上,当以点D、E、P、Q为顶点的四边形是平行四边形时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,BC=8,AB=6,经过点B和点D的两个动圆均与AC相切,且与AB、BC、AD、DC分别交于点G、H、E、F,则EF+GH的最小值是( )

A.6 B.8 C.9.6 D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB与CD相交于点O,OE⊥CD.
(1)若∠BOD=28°,求∠AOE的度数.
(2)若OF平分∠AOC,小明经探究发现:当∠BOD为锐角时,∠EOF的度数始终都是∠BOC度数的一半,请你判断他的发现是否正确,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
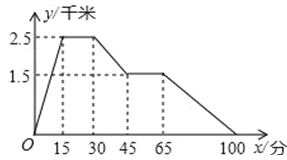
【题目】如图反映的是小刚从家里跑步去体育馆,在那里锻炼了一阵后又走到文具店去买笔,然后走回家,其中x表示时间,y表示小刚离家的距离.根据图象回答下列问题:
(1)体育场离小刚家 千米,小刚在体育场锻炼了 分钟.
(2)体育场离文具店 千米,小刚在文具店停留了 分钟.
(3)小刚从家跑步到体育场、从体育场走到文具店、从文具店散步回家的速度分别是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣x2+bx+c经过A(0,1)、B(4,3)两点.

(1)求抛物线的解析式;
(2)求tan∠ABO的值;
(3)过点B作BC⊥x轴,垂足为C,点M是抛物线上的一个动点,直线MN平行于y轴交直线AB于N,如果M、N、B、C为顶点的四边形是平行四边形,请直接写出M点的横坐标;
(4)已知点E为抛物线上位于第二象限内任一点,且E点横坐标为m,作边长为10的正方形EFGH,使EF∥x轴,点G在点E的右上方,那么,对于大于或等于﹣1的任意实数m,FG边与过A、B两点的直线都有交点,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,BD⊥AC于点D,E为BC上一点,过E点作EF⊥AC,垂足为F,过点D作DH∥BC交AB于点H.
(1)请你补全图形。
(2)求证:∠BDH=∠CEF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com