
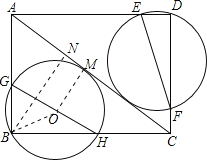
【题目】如图,在矩形ABCD中,BC=8,AB=6,经过点B和点D的两个动圆均与AC相切,且与AB、BC、AD、DC分别交于点G、H、E、F,则EF+GH的最小值是( )

A.6 B.8 C.9.6 D.10
【答案】C
【解析】
试题分析:如图,设GH的中点为O,过O点作OM⊥AC,过B点作BN⊥AC,垂足分别为M、N,根据∠B=90°可知,点O为过B点的圆的圆心,OM为⊙O的半径,BO+OM为直径,可知BO+OM≥BN,故当BN为直径时,直径的值最小,即直径GH也最小,同理可得EF的最小值.
解:如图,设GH的中点为O,
过O点作OM⊥AC,过B点作BN⊥AC,垂足分别为M、N,
在Rt△ABC中,BC=8,AB=6,
∴AC=![]() =10,
=10,
由面积法可知,BN![]() AC=AB
AC=AB![]() BC,
BC,
解得BN=4.8,
∵∠B=90°,
∴GH为⊙O的直径,点O为过B点的圆的圆心,
∵⊙O与AC相切,
∴OM为⊙O的半径,
∴BO+OM为直径,
又∵BO+OM≥BN,
∴当BN为直径时,直径的值最小,
此时,直径GH=BN=4.8,
同理可得:EF的最小值为4.8,
∴EF+GH的最小值是9.6.
故选C.


科目:初中数学 来源: 题型:
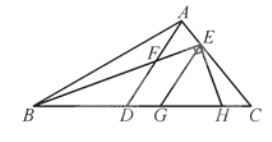
【题目】已知:如图,△ABC中,∠BAD=∠EBC,AD交BE于F.
(1)试说明 : ∠ABC=∠BFD ;
(2)若∠ABC=35°,EG∥AD,EH⊥BE,求∠HEG的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,ABCD中,E、F分别是边AB、CD的中点.
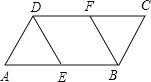
(1)求证:四边形EBFD是平行四边形;
(2)若AD=AE=2,∠A=60°,求四边形EBFD的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M,N.
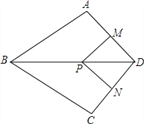
(1)求证:∠ADB=∠CDB;
(2)若∠ADC=90°,求证:四边形MPND是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,∠1=∠2,∠3=∠4,试说明![]() 的道理,以下是说明道理的过程,请将其填写完整,并在括号内填出所得结论的理由。
的道理,以下是说明道理的过程,请将其填写完整,并在括号内填出所得结论的理由。

∵∠1=∠2(已知),
![]() =∠1 ( ),
=∠1 ( ),
∴![]() =∠2 (等量代换),
=∠2 (等量代换),
∴![]() ( ),
( ),
∴![]() =
= ![]() ( ),
( ),
∵∠3=∠4(已知)
∴![]() -∠4=
-∠4= ![]() -∠3 (等式的基本性质),
-∠3 (等式的基本性质),
即∠( )= ![]()
∴![]() ( ).
( ).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com