
【题目】如图,在平面直角坐标系xOy中,已知四边形DOBC是矩形,且D(0,4),B(6,0).若反比例函数y= ![]() (x>0)的图象经过线段OC的中点A,交DC于点E,交BC于点F.设直线EF的解析式为y=k2x+b.
(x>0)的图象经过线段OC的中点A,交DC于点E,交BC于点F.设直线EF的解析式为y=k2x+b. 
(1)求反比例函数和直线EF的解析式;
(2)求△OEF的面积;
(3)请结合图象直接写出不等式k2x+b﹣ ![]() >0的解集.
>0的解集.
【答案】
(1)解:∵四边形DOBC是矩形,且D(0,4),B(6,0),
∴C点坐标为(6,4),
∵点A为线段OC的中点,
∴A点坐标为(3,2),
∴k1=3×2=6,
∴反比例函数解析式为y= ![]() ;
;
把x=6代入y= ![]() 得y=1,则F点的坐标为(6,1);
得y=1,则F点的坐标为(6,1);
把y=4代入y= ![]() 得x=
得x= ![]() ,则E点坐标为(
,则E点坐标为( ![]() ,4),
,4),
把F(6,1)、E( ![]() ,4)代入y=k2x+b得
,4)代入y=k2x+b得 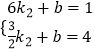 ,解得
,解得 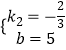 ,
,
∴直线EF的解析式为y=﹣ ![]() x+5;
x+5;
(2)解:△OEF的面积=S矩形BCDO﹣S△ODE﹣S△OBF﹣S△CEF
=4×6﹣ ![]() ×4×
×4× ![]() ﹣
﹣ ![]() ×6×1﹣
×6×1﹣ ![]() ×(6﹣
×(6﹣ ![]() )×(4﹣1)
)×(4﹣1)
= ![]() ;
;
(3)解:由图象得:不等式k2x+b﹣ ![]() >0的解集为
>0的解集为 ![]() <x<6.
<x<6.
【解析】(1)先利用矩形的性质确定C点坐标(6,4),再确定A点坐标为(3,2),则根据反比例函数图象上点的坐标特征得到k1=6,即反比例函数解析式为y= ![]() ;然后利用反比例函数解析式确定F点的坐标为(6,1),E点坐标为(
;然后利用反比例函数解析式确定F点的坐标为(6,1),E点坐标为( ![]() ,4),再利用待定系数法求直线EF的解析式;(2)利用△OEF的面积=S矩形BCDO﹣S△ODE﹣S△OBF﹣S△CEF进行计算;(3)观察函数图象得到当
,4),再利用待定系数法求直线EF的解析式;(2)利用△OEF的面积=S矩形BCDO﹣S△ODE﹣S△OBF﹣S△CEF进行计算;(3)观察函数图象得到当 ![]() <x<6时,一次函数图象都在反比例函数图象上方,即k2x+b>
<x<6时,一次函数图象都在反比例函数图象上方,即k2x+b> ![]() .
.


科目:初中数学 来源: 题型:
【题目】我市某中学艺术节期间,向学校学生征集书画作品.九年级美术李老师从全年级14个班中随机抽取了A、B、C、D 4个班,对征集到的作品的数量进行了分析统计,制作了如下两幅不完整的统计图. 
(1)李老师采取的调查方式是(填“普查”或“抽样调查”),李老师所调查的4个班征集到作品共件,其中B班征集到作品 , 请把图2补充完整.
(2)如果全年级参展作品中有4件获得一等奖,其中有2名作者是男生,2名作者是女生.现在要抽两人去参加学校总结表彰座谈会,求恰好抽中一男一女的概率.(要求用树状图或列表法写出分析过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣(x﹣1)2+c与x轴交于A,B(A,B分别在y轴的左右两侧)两点,与y轴的正半轴交于点C,顶点为D,已知A(﹣1,0).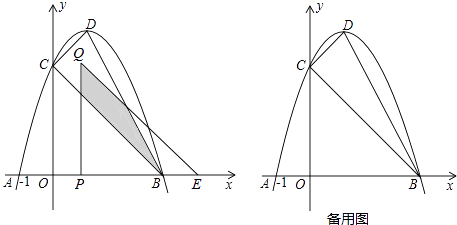
(1)求点B,C的坐标;
(2)判断△CDB的形状并说明理由;
(3)将△COB沿x轴向右平移t个单位长度(0<t<3)得到△QPE.△QPE与△CDB重叠部分(如图中阴影部分)面积为S,求S与t的函数关系式,并写出自变量t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是⊙O的内接四边形,∠ABC=2∠D,连接OA、OB、OC、AC,OB与AC相交于点E,若∠COB=3∠AOB,OC=2 ![]() ,则图中阴影部分面积是(结果保留π和根号)
,则图中阴影部分面积是(结果保留π和根号) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,AC、DC为弦,∠ACD=60°,P为AB延长线上的点,∠APD=30°. 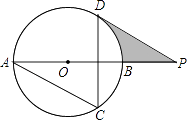
(1)求证:DP是⊙O的切线;
(2)若⊙O的半径为3cm,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小丽驾车从甲地到乙地.设她出发第xmin时的速度为ykm/h,图中的折线表示她在整个驾车过程中y与x之间的函数关系. 
(1)小丽驾车的最高速度是km/h;
(2)当20≤x≤30时,求y与x之间的函数关系式,并求出小丽出发第22min时的速度;
(3)如果汽车每行驶100km耗油10L,那么小丽驾车从甲地到乙地共耗油多少升?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com