
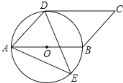
【题目】如图,四边形![]() 是平行四边形,以
是平行四边形,以![]() 为直径的
为直径的![]() 经过点
经过点![]() ,
,![]() 是
是![]() 上一点,且
上一点,且![]() .
.
![]() 求证:
求证:![]() 是
是![]() 的切线.
的切线.
![]() 若
若![]() 的半径为
的半径为![]() ,
,![]() ,求
,求![]() 的正弦值.
的正弦值.
【答案】(1)详见解析;(2)![]() 的正弦值是
的正弦值是![]() .
.
【解析】
(1)连接OD,证OD⊥CD即可.根据圆周角定理,∠AOD=90°,又AB∥CD,可得∠ODC=90°,得证;
(2)连接BE,则∠AEB=90°,∠ADE=∠ABE.在△ABE中根据三角函数定义求解.
(1)连接OD.则∠AOD=2∠AED=2×45°=90°.
∵四边形ABCD是平行四边形,∴AB∥DC,∴∠CDO=∠AOD=90°,∴OD⊥CD,∴CD与⊙O相切.
(2)连接BE,由圆周角定理,得∠ADE=∠ABE.
∵AB是⊙O的直径,∴∠AEB=90°,AB=2×3=6(cm).
在Rt△ABE中,sin∠ABE=![]() =
=![]() ,∴sin∠ADE=sin∠ABE=
,∴sin∠ADE=sin∠ABE=![]() .
.


 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:
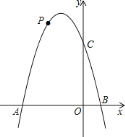
【题目】如图,已知二次函数![]() 的图象交
的图象交![]() 轴于点
轴于点![]() 和点
和点![]() ,交
,交![]() 轴于点
轴于点![]() .
.
![]() 求这个二次函数的表达式;
求这个二次函数的表达式;
![]() 若点
若点![]() 在第二象限内的抛物线上,求
在第二象限内的抛物线上,求![]() 面积的最大值和此时点
面积的最大值和此时点![]() 的坐标;
的坐标;
![]() 在平面直角坐标系内,是否存在点
在平面直角坐标系内,是否存在点![]() ,使
,使![]() ,
,![]() ,
,![]() ,
,![]() 四点构成平行四边形?若存在,直接写出点
四点构成平行四边形?若存在,直接写出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,四边形ABCD是正方形,∠MAN=45°,它的两边AM、AN分别交CB、DC与点M、N,连结MN,作AH⊥MN,垂足为点H
(1)如图1,猜想AH与AB有什么数量关系?并证明;
(2)如图2,已知∠BAC=45°,AD⊥BC于点D,且BD=2,CD=3,求AD的长;
小萍同学通过观察图①发现,△ABM和△AHM关于AM对称,△AHN和△ADN关于AN对称,于是她巧妙运用这个发现,将图形如图③进行翻折变换,解答了此题.你能根据小萍同学的思路解决这个问题吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小津去某风景区游览.小明从明桥出发沿景区公路骑自行车去陶公亭,同一时刻小津在霞山乘电动汽车出发沿同一公路去陶公亭,车速为![]() .他们出发后
.他们出发后![]() 时,离霞山的路程为
时,离霞山的路程为![]() ,
,![]() 为
为![]() 的函数图象如图所示.
的函数图象如图所示.
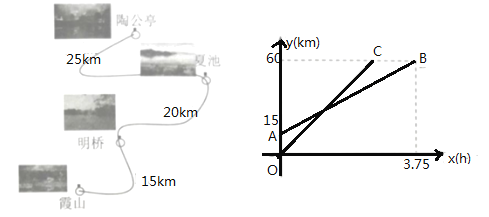
(1)求直线![]() 和直线
和直线![]() 的函数表达式;
的函数表达式;
(2)回答下列问题,并说明理由:
①当小津追上小明时,他们是否已过了夏池?
②当小津到达陶公亭时,小明离陶公亭还有多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,点D在AB上,AD=AC,AF⊥CD交CD于点E,交CB于点F,则CF的长是( )
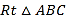
A.1.5B.1.8C.2D.2.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与x轴,y轴分别交于A,B两点,点
与x轴,y轴分别交于A,B两点,点![]() 为直线
为直线![]() 上一点,直线
上一点,直线![]() 过点C.
过点C.

![]() 求m和b的值;
求m和b的值;
![]() 直线
直线![]() 与x轴交于点D,动点P从点D开始以每秒1个单位的速度向x轴负方向运动
与x轴交于点D,动点P从点D开始以每秒1个单位的速度向x轴负方向运动![]() 设点P的运动时间为t秒.
设点P的运动时间为t秒.
①若点P在线段DA上,且![]() 的面积为10,求t的值;
的面积为10,求t的值;
②是否存在t的值,使![]() 为等腰三角形?若存在,直接写出t的值;若不存在,请说明理由.
为等腰三角形?若存在,直接写出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年平昌冬奥会在2月9日到25日在韩国平昌郡举行,为了调查中学生对冬奥会比赛项目的了解程度,某中学在学生中做了一次抽样调查,调查结果共分为四个等级:A、非常了解B、比较了解C、基本了解D、不了解.根据调查统计结果,绘制了如图所示的不完整的三种统计图表.
对冬奥会了解程度的统计表
对冬奥会的了解程度 | 百分比 |
A非常了解 | 10% |
B比较了解 | 15% |
C基本了解 | 35% |
D不了解 | n% |
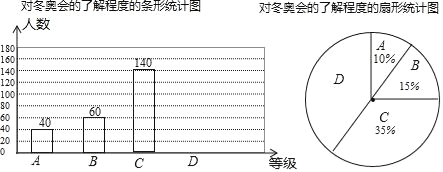
(1)n= ;
(2)扇形统计图中,D部分扇形所对应的圆心角是 ;
(3)请补全条形统计图;
(4)根据调查结果,学校准备开展冬奥会的知识竞赛,某班要从“非常了解”程度的小明和小刚中选一人参加,现设计了如下游戏来确定谁参赛,具体规则是:把四个完全相同的乒乓球标上数字1,2,3,4然后放到一个不透明的袋中,一个人先从袋中摸出一个球,另一人再从剩下的三个球中随机摸出一个球,若摸出的两个球上的数字和为偶数,则小明去,否则小刚去,请用画树状图或列表的方法说明这个游戏是否公平.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,
,![]() 于
于![]() ,
,![]() 平分
平分![]() ,且
,且![]() 于
于![]() ,与
,与![]() 相交于点
相交于点![]() ,
,![]() 是
是![]() 边的中点,连接
边的中点,连接![]() 与
与![]() 相交于点
相交于点![]() ,下列结论正确的有( )个
,下列结论正确的有( )个
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 是等腰三角形;⑤
是等腰三角形;⑤![]() .
.

A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com