
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,点D在AB上,AD=AC,AF⊥CD交CD于点E,交CB于点F,则CF的长是( )
A.1.5B.1.8C.2D.2.5
【答案】A
【解析】
连接DF,由勾股定理求出AB=5,由等腰三角形的性质得出CE=DE,由线段垂直平分线的性质得出CF=DF,由SSS证明△ADF≌△ACF,得出∠ADF=∠ACF=∠BDF=90°,设CF=DF=x,则BF=4-x,在Rt△BDF中,由勾股定理得出方程,解方程即可.
解:连接DF,如图所示:
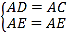
∵在Rt△ABC中,∠ACB=90°,AC=3,BC=4,
∴![]()
∵AD=AC=3,AF⊥CD,
∴CE=DE,BD=AB-AD=2,∴CF=DF,
在△ADF和△ACF中,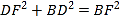
∴△ADF≌△ACF(SSS),
∴∠ADF=∠ACF=90°,
∴∠BDF=90°,
设CF=DF=x,则BF=4-x,
在Rt△BDF中,由勾股定理得: ![]() ,
,
即![]() ,
,
解得:x=1.5;
∴CF=1.5;
故选:A.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,Rt△OAB的顶点A(-2,4)在抛物线y=ax2上,将Rt△OAB绕点O顺时针旋转90°,得到△OCD,边CD与该抛物线交于点P,则点P的坐标为( )
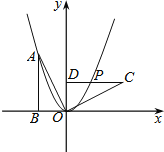
A. (![]() ,
, ![]() ) B. (2,2) C. (
) B. (2,2) C. (![]() ,2) D. (2,
,2) D. (2, ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形ABCD的边CD上适当选定一点E,沿直线AE把△ADE折叠,使点D恰好落在边BC上的点F处.已知AB=6cm,△ABF的面积是24cm2.
(1)求BF的长;
(2)求AD的长;
(3)求点E与点C的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图已知![]() 的三个顶点坐标分别是
的三个顶点坐标分别是![]() ,
,![]() ,
,![]() .
.
(1)将![]() 向上平移4个单位长度得到
向上平移4个单位长度得到![]() ,请画出
,请画出![]() ;
;
(2)请画出与![]() 关于
关于![]() 轴对称的
轴对称的![]() ;
;
(3)请写出![]() 的坐标,并用恰当的方式表示线段
的坐标,并用恰当的方式表示线段![]() 上任意一点的坐标.
上任意一点的坐标.
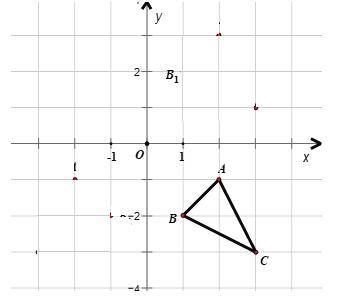
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大学生利用暑假40天社会实践参与了一家网店经营,了解到一种成本为20元/件的新型商品在第x天销售的相关信息如下表所示.
销售量p(件) | P=50—x |
销售单价q(元/件) | 当1≤x≤20时,q=30+ 当21≤x≤40时,q=20+ |
(1)求该网店第x天获得的利润y关于x的函数关系式;
(2)这40天中该网店第几天获得的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某游泳馆推出了两种收费方式.
方式一:顾客先购买会员卡,每张会员卡200元,仅限本人一年内使用,凭卡游泳,每次游泳再付费30元.
方式二:顾客不购买会员卡,每次游泳付费40元.
设小亮在一年内来此游泳馆的次数为x次,选择方式一的总费用为y1(元),选择方式二的总费用为y2(元).
(1)请分别写出y1,y2与x之间的函数表达式.
(2)若小亮一年内来此游泳馆的次数为15次,选择哪种方式比较划算?
(3)若小亮计划拿出1400元用于在此游泳馆游泳,采用哪种付费方式更划算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG,动点P从点A出发,沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B时停止(不含点A和点B),则△ABP的面积S随着时间t变化的函数图象大致是( )

A. 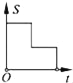 B.
B. 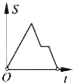 C.
C. 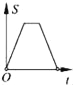 D.
D. 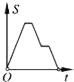
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义:如果一个等腰三角形有一条边长是3,那么这个三角形称作帅气等腰三角形.已知![]() 中,
中,![]() ,
,![]() ,
,![]() ,在
,在![]() 所在平面内画一条直线,将
所在平面内画一条直线,将![]() 分割成两个三角形,若其中一个三角形是帅气等腰三角形,则这样的直线最多可画( )
分割成两个三角形,若其中一个三角形是帅气等腰三角形,则这样的直线最多可画( )
A.0条B.1条C.2条D.3条
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com