
【题目】如图,在长方形ABCD的边CD上适当选定一点E,沿直线AE把△ADE折叠,使点D恰好落在边BC上的点F处.已知AB=6cm,△ABF的面积是24cm2.
(1)求BF的长;
(2)求AD的长;
(3)求点E与点C的距离.

【答案】(1)8cm;(2)10cm;(3)![]() cm
cm
【解析】
(1)由在长方形ABCD中,AB=6cm,△ABF的面积是24cm2,即可求得BF的长;
(2)由(1),易得AD=AF,DE=EF,即可求得AF的长,然后得出AD的长;
(3)首先设EC=xcm,则EF=DE=(6﹣x)cm.由勾股定理得:CE2+CF2=EF2求出x的值即可得出答案.
(1)∵ABCD是长方形,
∴△ABF是直角三角形,
∵△ABF面积是24cm2,
∴![]() ABBF=24.
ABBF=24.
∵AB=6cm,
∴BF=8cm;
(2)由题意知,△ADE和△AFE重合,
则△ADE≌△AFE,
则AD=AF,DE=EF.
在Rt△ABF中,由勾股定理得![]() (cm).
(cm).
则AD=10cm;
(3)∵BC=AD=10cm,
∴CF=BC﹣BF=2cm.
设EC=xcm,则EF=DE=(6﹣x)cm.
由勾股定理得:CE2+CF2=EF2,
∴x2+22=(6﹣x)2,
解得:![]() ,
,
∴点E与点C间的距离是![]() cm.
cm.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:初中数学 来源: 题型:
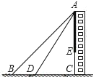
【题目】如图,![]() 是我市某大楼的高,在地面上
是我市某大楼的高,在地面上![]() 点处测得楼顶
点处测得楼顶![]() 的仰角为
的仰角为![]() ,沿
,沿![]() 方向前进
方向前进![]() 米到达
米到达![]() 点,测得
点,测得![]() .现打算从大楼顶端
.现打算从大楼顶端![]() 点悬挂一幅庆祝建国
点悬挂一幅庆祝建国![]() 周年的大型标语,若标语底端距地面
周年的大型标语,若标语底端距地面![]() ,请你计算标语
,请你计算标语![]() 的长度应为多少?
的长度应为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】因为一次函数![]() 与
与![]() 的图象关于
的图象关于![]() 轴对称,所以我们定义:函数
轴对称,所以我们定义:函数![]() 与互为
与互为![]() “镜子”函数.
“镜子”函数.
(1)请直接写出函数![]() 的“镜子”函数:________.
的“镜子”函数:________.
(2)如图,一对“镜子”函数![]() 与
与![]() 的图象交于点
的图象交于点![]() ,分别与
,分别与![]() 轴交于
轴交于![]() 两点,且AO=BO,△ABC的面积为
两点,且AO=BO,△ABC的面积为![]() ,求这对“镜子”函数的解析式.
,求这对“镜子”函数的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD沿着直线BD折叠,使点C落在C/处,BC/交AD于E,AD=8,AB=4,DE的长=________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,四边形ABCD是正方形,∠MAN=45°,它的两边AM、AN分别交CB、DC与点M、N,连结MN,作AH⊥MN,垂足为点H
(1)如图1,猜想AH与AB有什么数量关系?并证明;
(2)如图2,已知∠BAC=45°,AD⊥BC于点D,且BD=2,CD=3,求AD的长;
小萍同学通过观察图①发现,△ABM和△AHM关于AM对称,△AHN和△ADN关于AN对称,于是她巧妙运用这个发现,将图形如图③进行翻折变换,解答了此题.你能根据小萍同学的思路解决这个问题吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,AD=6,AB=10,∠A=30°,以点A为圆心,AD的长为半径画弧交AB于点E,连接CE.

(1)求弧DE的长;
(2)求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,点D在AB上,AD=AC,AF⊥CD交CD于点E,交CB于点F,则CF的长是( )
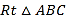
A.1.5B.1.8C.2D.2.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com