
【题目】已知二次函数![]() 的部分图象如图所示,则关于x的一元二次方程
的部分图象如图所示,则关于x的一元二次方程![]() 的解为_________________
的解为_________________
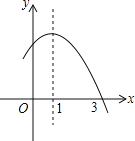
【答案】x>3或x<-1
【解析】
首先把(3,0)代入二次函数y=-x2+2x+m可得m的值,然后再解-x2+2x+3=0可得解;根据二次函数y=-x2+2x+m,y<0时,图象在x轴下方可得x>3或x<-1,进而可得不等式-x2+2x+m>0的解集.
解:根据图象可知,二次函数y=-x2+2x+m的部分图象经过点(3,0),所以该点适合方程y=-x2+2x+m,代入,得
-32+2×3+m=0,
解得m=3,
把m=3代入一元二次方程-x2+2x+m=0,得
-x2+2x+3=0,
解得x1=3,x2=-1;
∵二次函数y=-x2+2x+m,y<0时,图象在x轴下方,
∴y<0时,x>3或x<-1,
∴不等式-x2+2x+m<0的解集x>3或x<-1.
故答案为:x>3或x<-1.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:
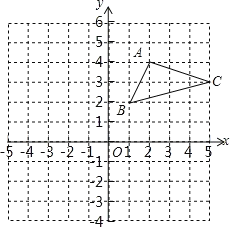
【题目】如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4)
(1)画出△ABC关于y轴对称的△A1B1C1;
(2)写出点A1的坐标;
(3)画出△A1B1C1向下平移3个单位长度所得的△A2B2C2;
(4)在x轴上找一点P,使PB+PC的和最小(标出点P即可,不用求点P的坐标)
查看答案和解析>>
科目:初中数学 来源: 题型:
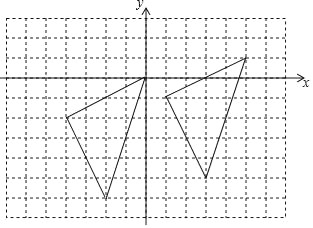
【题目】在如图的方格中,△OAB的顶点坐标分别为O(0,0)、A(﹣2,﹣1)、B(﹣1,﹣3),△O1A1B1与△OAB是关于点P为位似中心的位似图形.
(1)在图中标出位似中心P的位置,并写出点P的坐标及△O1A1B1与△OAB的相似比;
(2)以原点O为位似中心,在y轴的左侧画出△OAB的一个位似△OA2B2,使它与△OAB的位似比为2:1,并写出点B的对应点B2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△OAB的顶点A(-2,4)在抛物线y=ax2上,将Rt△OAB绕点O顺时针旋转90°,得到△OCD,边CD与该抛物线交于点P,则点P的坐标为( )
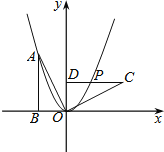
A. (![]() ,
, ![]() ) B. (2,2) C. (
) B. (2,2) C. (![]() ,2) D. (2,
,2) D. (2, ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年是“精准扶贫”攻坚关键年,某扶贫工作队为对口扶贫村引进建立了一村集体企业,并无偿提供一笔无息贷款作为启动资金,双方约定:①企业生产出的产品全部由扶贫工作队及时联系商家收购;②企业从生产销售的利润中,要保证按时发放工人每月最低工资32000元.已知该企业生产的产品成本为20元/件,月生产量y(千件)与出厂价x(元)(25≤x≤50)的函数关系可用图中的线段AB和BC表示,其中AB的解析式为y=﹣![]() x+m(m为常数).
x+m(m为常数).
(1)求该企业月生产量y(千件)与出厂价x(元)之间的函数关系式,并写出自变量x的取值范围.
(2)当该企业生产出的产品出厂价定为多少元时,月利润W(元)最大?最大利润是多少?[月利润=(出厂价﹣成本)×月生产量﹣工人月最低工资].

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】房价上涨成为热点问题.据统计,某地房价由8月份房子每平方均价由5000元涨到10月份每平方均价7200元.
(1)求该地这两个月房价的平均增长率;
(2)按此速度上涨,11月房价每平方能否超过8500元,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
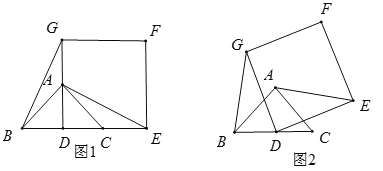
【题目】(1)观察猜想
如图(1),在△ABC中,∠BAC=90°,AB=AC,点D是BC的中点.以点D为顶点作正方形DEFG,使点A,C分别在DG和DE上,连接AE,BG,则线段BG和AE的数量关系是_____;
(2)拓展探究
将正方形DEFG绕点D逆时针方向旋转一定角度后(旋转角度大于0°,小于或等于360°),如图2,则(1)中的结论是否仍然成立?如果成立,请予以证明;如果不成立,请说明理由.
(3)解决问题
若BC=DE=2,在(2)的旋转过程中,当AE为最大值时,直接写出AF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形ABCD的边CD上适当选定一点E,沿直线AE把△ADE折叠,使点D恰好落在边BC上的点F处.已知AB=6cm,△ABF的面积是24cm2.
(1)求BF的长;
(2)求AD的长;
(3)求点E与点C的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某游泳馆推出了两种收费方式.
方式一:顾客先购买会员卡,每张会员卡200元,仅限本人一年内使用,凭卡游泳,每次游泳再付费30元.
方式二:顾客不购买会员卡,每次游泳付费40元.
设小亮在一年内来此游泳馆的次数为x次,选择方式一的总费用为y1(元),选择方式二的总费用为y2(元).
(1)请分别写出y1,y2与x之间的函数表达式.
(2)若小亮一年内来此游泳馆的次数为15次,选择哪种方式比较划算?
(3)若小亮计划拿出1400元用于在此游泳馆游泳,采用哪种付费方式更划算?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com