
【题目】如图,在正方形![]() 中,点
中,点![]() 、
、![]() 分别为边
分别为边![]() 、
、![]() 上两点,
上两点,![]() ,过点
,过点![]() 作
作![]() ,且点
,且点![]() 为边
为边![]() 延长线上一点.
延长线上一点.
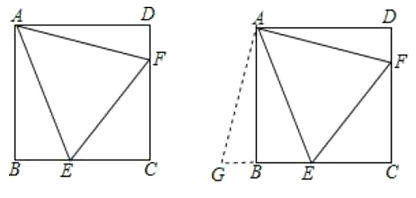
(1)![]() 吗?说明理由.
吗?说明理由.
(2)若线段![]() ,
,![]() ,求线段
,求线段![]() 的长度.
的长度.
(3)若![]() ,
,![]() ,求线段
,求线段![]() 的长度.
的长度.
【答案】(1)见解析;(2)12;(3)EF=10
【解析】
(1)通过正方形的性质可得AB=AD、∠ABG =∠D,即可证明△GAB≌△FAD.
(2)通过证明△GAE≌△FAE(SAS)和△GAB≌△FAD,可得EF=GE和GB=DF,从而可得EF=GE=GB+BE=FD+BE=8+4=12.
(3)设EF=x,则BE=GEBG=x4,根据EC=BCBE可得EC=12(x4)=16x,根据勾股定理列方程求解即可.
(1)全等.
证明:∵四边形ABCD为正方形
∴AB=AD,∠ABE=∠D=90![]() ,
,
∴∠ABG =90![]() =∠D
=∠D
在△ABG和△ADF中,
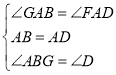
∴△GAB≌△FAD.
(2)∵∠BAD=90![]() ,∠EAF=45
,∠EAF=45![]()
∴∠DAF+∠BAE=45![]()
∵△GAB≌△FAD
∴∠GAB=∠FAD,AG=AF
∴∠GAB+∠BAE=45![]()
∴∠GAE=45
∴∠GAE=∠EAF
在△GAE和△FAE中
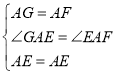
∴△GAE≌△FAE(SAS)
∴EF=GE.
∵△GAB≌△FAD
∴GB=DF
∴EF=GE=GB+BE=FD+BE=8+4=12.
(3)设EF=x,则BE=GEBG=x4.
∵EC=BCBE,
∴EC=12(x4)=16x.
在Rt△EFC中,依据勾股定理可知:
EF2=FC2+EC2,
即(16x) 2+82=x2,
解得:x=10.
∴EF=10.


科目:初中数学 来源: 题型:
【题目】阅读下列两段材料,回答问题:
材料一:A(x1.y1),B(x2.y2)的中点坐标为(![]() ,
,![]() ) 例如,点(1,5),(3,-1)的中点坐标为(
) 例如,点(1,5),(3,-1)的中点坐标为(![]() ,
,![]() ),即(2, 2)
),即(2, 2)
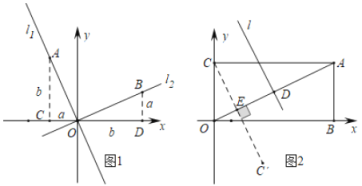
材料二:如图1,正比例函数l1:y=k1x和l2:y=k2x的图像相互垂直,分别在l1和l2上取点A、B,使得AO=BO.分别过点A、B作x轴的垂线,垂足分别为点C、D.显然△AOC≌△ OBD.设OC=BD=a,AC=OD=b.则A(-a,b),B(b,a).于是![]() ,所以k1k2的值为一个常数.
,所以k1k2的值为一个常数.
(1)在材料二中,k1k2=____ (写出这个常数具体的值) ;
(2)如图,在矩形OBAC中A(4,2),点D是OA中点,用两段材料的结论,求点D的坐标和OA的垂直平分线l的解析式;
(3)若点C’ 与点C关于OA对称,用两段材料的结论,求点C'的坐标,
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填幻方:将1、2、3、4、5、6、7、8、9这九个数字分别填在如图所示的九个空格中,要求每一行从左到右的数字逐渐增大,每一列从上到下的数字也逐渐增大.当数字2、4固定在图中所示的位置时,按规则填写空格,所有可能出现的结果有( )
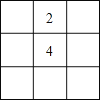
A.4种B.6种C.8种D.9种
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知点A、B是反比例函数y=﹣![]() 上在第二象限内的分支上的两个点,点C(0,3),且△ABC满足AC=BC,∠ACB=90°,则线段AB的长为__.
上在第二象限内的分支上的两个点,点C(0,3),且△ABC满足AC=BC,∠ACB=90°,则线段AB的长为__.

【答案】![]()
【解析】过点A作AD⊥y轴于点D,过点B作BE⊥y轴于点E,过点A作AF⊥BE轴于点F,如图所示.

∵∠ACB=90°,
∴∠ACD+∠BCE=90°,
又∵AD⊥y轴,BE⊥y轴,
∴∠ACD+∠CAD=90°,∠BCE+∠CBE=90°,
∴∠ACD=∠CBE,∠BCE=∠CAD.
在△ACD和△CBE中,由 ,
,
∴△ACD≌△CBE(ASA).
设点B的坐标为(m,﹣![]() )(m<0),则E(0,﹣
)(m<0),则E(0,﹣![]() ),点D(0,3﹣m),点A(﹣
),点D(0,3﹣m),点A(﹣![]() ﹣3,3﹣m),
﹣3,3﹣m),
∵点A(﹣![]() ﹣3,3﹣m)在反比例函数y=﹣
﹣3,3﹣m)在反比例函数y=﹣![]() 上,
上,
 ,解得:m=﹣3,m=2(舍去).
,解得:m=﹣3,m=2(舍去).
∴点A的坐标为(﹣1,6),点B的坐标为(﹣3,2),点F的坐标为(﹣1,2),
∴BF=2,AF=4,
![]()
故答案为:2![]() .
.
【点睛】
过点A作AD⊥y轴于点D,过点B作BE⊥y轴于点E,过点A作AF⊥BE轴于点F,根据角的计算得出“∠ACD=∠CBE,∠BCE=∠CAD”,由此证出△ACD≌△CBE;再设点B的坐标为(m,﹣![]() ),由三角形全等找出点A的坐标,将点A的坐标代入到反比例函数解析式中求出m的值,将m的值代入A,B点坐标即可得出点A,B的坐标,并结合点A,B的坐标求出点F的坐标,利用勾股定理即可得出结论.
),由三角形全等找出点A的坐标,将点A的坐标代入到反比例函数解析式中求出m的值,将m的值代入A,B点坐标即可得出点A,B的坐标,并结合点A,B的坐标求出点F的坐标,利用勾股定理即可得出结论.
【题型】填空题
【结束】
18
【题目】二次函数y=x2+(2m+1)x+(m2﹣1)有最小值﹣2,则m=________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线l:y=﹣![]() x+6交y轴于点A,与x轴交于点B,过A、B两点的抛物线m与x轴的另一个交点为C,(C在B的左边),如果BC=5,求抛物线m的解析式,并根据函数图像指出当m的函数值大于0的函数值时x的取值范围.
x+6交y轴于点A,与x轴交于点B,过A、B两点的抛物线m与x轴的另一个交点为C,(C在B的左边),如果BC=5,求抛物线m的解析式,并根据函数图像指出当m的函数值大于0的函数值时x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角标系中,△ABC的三个顶点坐标为A(-3,1)、B(-4,-3)、C(-2,-4),△ABC绕原点顺时针旋转180°,得到△A1B1C1再将△A1B1C1向左平移5个单位得到△A2B2C2.
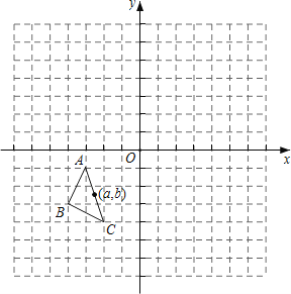
(1)画出△A1B1C1,并写出点A的对应点A1的坐标;
(2)画出△A2B2C2,并写出点A的对应点A2的坐标;
(3)P(a,b)是△ABC的边AC上一点,△ABC经旋转,平移后点P的对应点分别为P1、P2,请直接写出点P2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C、D是圆上两点,且OD∥AC,OD与BC交于点E.

(1)求证:E为BC的中点;
(2)若BC=8,DE=3,求AB的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数 y=ax2+bx+c(a≠0)的图象与 x 轴交于 A、B 两点,与 y 轴交于点 C,且对称轴为直线 x=1, 点 B 的坐标为(-1,0).则下面的五个结论:①2a+b=0;②abc>0;③当 y<0 时,x<-1 或 x>2;④c<4b;⑤ a+b>m(am+b)(m≠1),其中正确的个数是( )
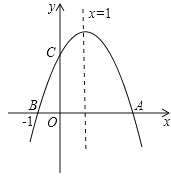
A. 2 个 B. 3个 C. 4 个 D. 5 个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com