
【题目】阅读下列两段材料,回答问题:
材料一:A(x1.y1),B(x2.y2)的中点坐标为(![]() ,
,![]() ) 例如,点(1,5),(3,-1)的中点坐标为(
) 例如,点(1,5),(3,-1)的中点坐标为(![]() ,
,![]() ),即(2, 2)
),即(2, 2)
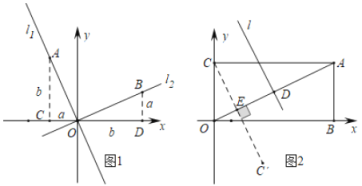
材料二:如图1,正比例函数l1:y=k1x和l2:y=k2x的图像相互垂直,分别在l1和l2上取点A、B,使得AO=BO.分别过点A、B作x轴的垂线,垂足分别为点C、D.显然△AOC≌△ OBD.设OC=BD=a,AC=OD=b.则A(-a,b),B(b,a).于是![]() ,所以k1k2的值为一个常数.
,所以k1k2的值为一个常数.
(1)在材料二中,k1k2=____ (写出这个常数具体的值) ;
(2)如图,在矩形OBAC中A(4,2),点D是OA中点,用两段材料的结论,求点D的坐标和OA的垂直平分线l的解析式;
(3)若点C’ 与点C关于OA对称,用两段材料的结论,求点C'的坐标,
【答案】(1)-1;(2)D(2,1),OA的垂直平分线l的解析式为:y=-2x+5;(3)C′(![]() ).
).
【解析】
(1)根据材料二中,![]() ,即可得到答案;
,即可得到答案;
(2)根据线段中点坐标公式,可得D的坐标,求出直线OA的解析式为:y=![]() x,可设OA的垂直平分线l的解析式为:y=-2x+b,根据待定系数法,即可得到答案;
x,可设OA的垂直平分线l的解析式为:y=-2x+b,根据待定系数法,即可得到答案;
(3)由C,C′关于OA对称,可设CC′所在直线的解析式为:y=-2x+b,根据待定系数法,即可求出CC′所在直线的解析式,进而求出E的坐标,根据中点坐标公式,即可得到C′的坐标.
(1)∵![]() ,
,
∴k1k2=-1,
故答案是:-1;
(2)∵O(0,0),A(4,2),
∴D(![]() ),即:D(2,1),
),即:D(2,1),
设直线OA的解析式为:y=kx,
把A(4,2)代入得:2=4k,解得:k=![]() ,
,
∴直线OA的解析式为:y=![]() x,
x,
设OA的垂直平分线l的解析式为:y=-2x+b,
把D(2,1)代入得:1=-2×2+b,解得:b=5,
∴OA的垂直平分线l的解析式为:y=-2x+5;
(3)∵C,C′关于OA对称,
∴CC′⊥OA,E是CC′的中点,
设CC′所在直线的解析式为:y=-2x+b,
把C(0,2)代入解析式得:b=2,
∴CC′所在直线的解析式为:y=-2x+2,
联立 ,解得:
,解得:![]() ,
,
∴E(![]() ),
),
∴C′(![]() ),即:C′(
),即:C′(![]() ).
).


 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
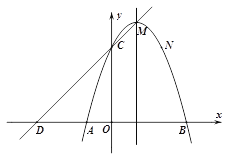
【题目】如图,已知抛物线的顶点坐标为M(1,4),且经过点N(2,3),与x轴交于A、B两点(点A在点B左侧),与y轴交于点C.
(1)求抛物线的解析式;
(2)若直线y=kx+t经过C、M两点,且与x轴交于点D,试证明四边形CDAN是平行四边形;
(3)点P在抛物线的对称轴x=1上运动,请探索:在x轴上方是否存在这样的P点,使以P为圆心的圆经过A、B两点,并且与直线CD相切?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
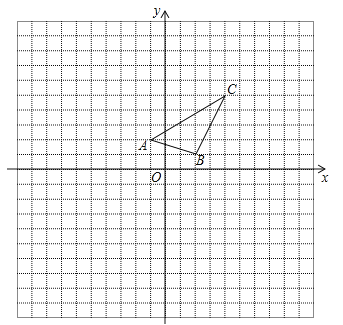
【题目】如图,在边长为1的正方形网格中建立平面直角坐标系,已知△ABC三个顶点分别为A(﹣1,2)、B(2,1)、C(4,5).
(1)画出△ABC关于x对称的△A1B1C1;
(2)以原点O为位似中心,在x轴的上方画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2,并求出△A2B2C2的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为鼓励大学毕业生自主创业,某市政府出台了相关政策:由政府协调,本市企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担.李明按照相关政策投资销售本市生产的一种新型节能灯.已知这种节能灯的成本价为每件10元,出厂价为每件12元,每月销售量y(件)与销售单价x(元)之间的关系近似满足一次函数:y=-10x+500.
(1)李明在开始创业的第一个月将销售单价定为20元,那么政府这个月为他承担的总差价为多少元?
(2)设李明获得的利润为W(元),当销售单价定为多少元时,每月可获得最大利润?
(3)物价部门规定,这种节能灯的销售单价不得高于25元.如果李明想要每月获得的利润不低于3000元,那么政府为他承担的总差价最少为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B在反比例函数![]() (x>0)的图象上,点C,D在反比例函数
(x>0)的图象上,点C,D在反比例函数![]() (k>0)的图象上,AC∥BD∥y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为
(k>0)的图象上,AC∥BD∥y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为![]() ,则k的值为( )
,则k的值为( )
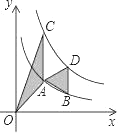
A. 3 B. 4 C. 2 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在边长为1个单位长度的小正方形组成的网格中,建立如图所示的平面直角坐标系△ABC是格点三角形(顶点在网格线的交点上)
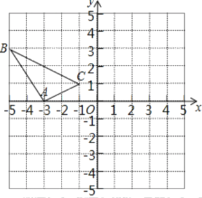
(1)先作△ABC关于原点O成中心对称的![]() ,再把
,再把![]() 向上平移4个单位长度得到
向上平移4个单位长度得到![]() ;
;
(2)△ABC可以经过一次旋转变换得到![]() ,旋转角的大小为多少?写出旋转中心的坐标.
,旋转角的大小为多少?写出旋转中心的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程或方程组解应用题:
为了响应“十三五”规划中提出的绿色环保的倡议,某校文印室提出了每个人都践行“双面打印,节约用纸”.已知打印一份资料,如果用A4厚型纸单面打印,总质量为400克,将其全部改成双面打印,用纸将减少一半;如果用A4薄型纸双面打印,这份资料的总质量为160克,已知每页薄型纸比厚型纸轻0.8克,求A4薄型纸每页的质量.(墨的质量忽略不计)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形![]() 中,点
中,点![]() 、
、![]() 分别为边
分别为边![]() 、
、![]() 上两点,
上两点,![]() ,过点
,过点![]() 作
作![]() ,且点
,且点![]() 为边
为边![]() 延长线上一点.
延长线上一点.
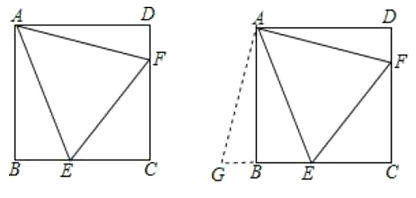
(1)![]() 吗?说明理由.
吗?说明理由.
(2)若线段![]() ,
,![]() ,求线段
,求线段![]() 的长度.
的长度.
(3)若![]() ,
,![]() ,求线段
,求线段![]() 的长度.
的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com