
【题目】在平面直角坐标系xOy中,直线y=kx+4(k≠0)与y轴交于点A.
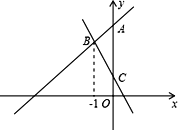
(1)如图,直线y=﹣2x+1与直线y=kx+4(k≠0)交于点B,与y轴交于点C,点B的横坐标为-1.
①求点B的坐标及k的值;
②直线y=﹣2x+1与直线y=kx+4与y轴所围成的△ABC的面积等于 ;
(2)直线y=kx+4(k≠0)与x轴交于点E(x 0 ,0),若﹣2<x 0 <﹣1,求k的取值范围.
【答案】(1)①B(-1,3);k=1;②、1.5;(2)2<k<4.
【解析】试题分析:(1)将点B的横坐标代入y=-2x+1得出点B的纵坐标,将点B的坐标代入y=kx+4求出k的值;根据解析式求出A、C的坐标,然后进行计算;(2)用k的代数式表示点E的横坐标,然后根据不等式求出k的取值.
试题解析:(1)①将x=-1代入y=-2x+1得:y=-2×(-1)+1=3,∴点B的坐标为(-1,3)
将点B的坐标代入y=kx+4得:-k+4=3 解得:k=1
②、根据题意可得:点A的坐标为(0,4) 点C的坐标为(0,1) ∴AC=4-1=3 ∴S=3×1÷2=1.5
(2)当y=0时,x=-![]() 即
即![]() =-
=-![]() 即-2<-
即-2<-![]() <-1 解得:2<k<4.
<-1 解得:2<k<4.


科目:初中数学 来源: 题型:
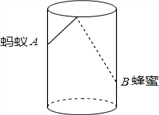
【题目】如图,圆柱形容器高为18cm,底面周长为24cm,在杯内壁离杯底4cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿2cm与蜂蜜相对的点A处,为了吃到蜂蜜,蚂蚁从外壁A处沿着最短路径到达内壁B处。
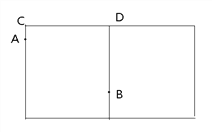
(1)右图是杯子的侧面展开图,请在杯沿CD上确定一点P,使蚂蚁沿A-P-B路线爬行,距离最短。
(2)结合右图,求出蚂蚁爬行的最短路径长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题探究】用同样大小的小正方形纸片,按下图的方式拼正方形.
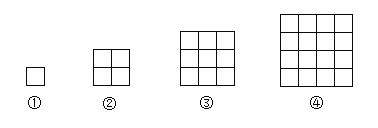
规律:第①个图形中有1个小正方形;
第②个图形比第①个图形多3个小正方形;
第③个图形比第②个图形多5个小正方形;
……
第(n+1)个图形比第n个图形多________个小正方形.
可发现以下结论:(1)1+3+5+…+(2n-1)= ____________.
(2)(n+1)2-n2 = ____________.
【知识运用】
运用一:如果一个数可用几个连续的奇数和来表示,我们称这个数为“好数”,例如:9=1+3+5,32=5+7+9+11,则称9和32都是“好数”.
请尝试将下列“好数”用连续奇数的和表示出来:
(1)![]() =_____________________________________.
=_____________________________________.
(2)99 =_____________________________________.
运用二:利用上面的结论,请计算![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com