
ЁОЬтФПЁПЁОЮЪЬтЬНОПЁПгУЭЌбљДѓаЁЕФаЁе§ЗНаЮжНЦЌЃЌАДЯТЭМЕФЗНЪНЦДе§ЗНаЮЃЎ
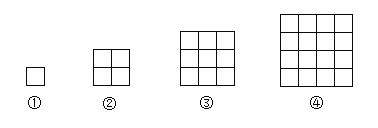
ЙцТЩЃКЕкЂйИіЭМаЮжага1ИіаЁе§ЗНаЮЃЛ
ЕкЂкИіЭМаЮБШЕкЂйИіЭМаЮЖр3ИіаЁе§ЗНаЮЃЛ
ЕкЂлИіЭМаЮБШЕкЂкИіЭМаЮЖр5ИіаЁе§ЗНаЮЃЛ
ЁЁ
Ек(n+1)ИіЭМаЮБШЕкnИіЭМаЮЖр________ИіаЁе§ЗНаЮЃЎ
ПЩЗЂЯжвдЯТНсТлЃКЃЈ1ЃЉ1+3+5+Ё+ЃЈ2nЃ1ЃЉ= ____________ЃЎ
ЃЈ2ЃЉ(n+1)2Ѓn2 = ____________ЃЎ
ЁОжЊЪЖдЫгУЁП
дЫгУвЛЃКШчЙћвЛИіЪ§ПЩгУМИИіСЌајЕФЦцЪ§КЭРДБэЪОЃЌЮвУЧГЦетИіЪ§ЮЊЁАКУЪ§ЁБЃЌР§ШчЃК9=1+3+5ЃЌ32=5+7+9+11ЃЌдђГЦ9КЭ32ЖМЪЧЁАКУЪ§ЁБЃЎ
ЧыГЂЪдНЋЯТСаЁАКУЪ§ЁБгУСЌајЦцЪ§ЕФКЭБэЪОГіРДЃК
ЃЈ1ЃЉ![]() =_____________________________________ЃЎ
=_____________________________________ЃЎ
ЃЈ2ЃЉ99 =_____________________________________ЃЎ
дЫгУЖўЃКРћгУЩЯУцЕФНсТлЃЌЧыМЦЫу![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ЁОД№АИЁП ЃЈ2n+1ЃЉ n2 2n+1 1+3+5+7+9+11+13 3+5+7+9+11+13+15+17+19 Лђ 31+33+35
ЁОНтЮіЁПЪдЬтЗжЮіЃК
ЁОЮЪЬтЬНОПЁП
ЕкЂкИіЭМаЮБШЕкЂйИіЭМаЮЖр3ЃН2ЁС2Ѓ1ИіаЁе§ЗНаЮЃЛ
ЕкЂлИіЭМаЮБШЕкЂкИіЭМаЮЖр5ЃН2ЁС3Ѓ1ИіаЁе§ЗНаЮЃЛ
ЁЁ
ЕкnИіЭМаЮБШЕкnЃ1ИіЭМаЮЖр2nЃ1ИіаЁе§ЗНаЮ
Ек(nЃЋ1)ИіЭМаЮБШЕкnИіЭМаЮЖр2(nЃЋ1)Ѓ1ЃН2nЃЋ1ИіаЁе§ЗНаЮЃЛ
ЃЈ1ЃЉ1ЃЋ3ЃЋ5ЃЋЁЃЋЃЈ2nЃ1ЃЉБэЪОЕкnИіЭМаЮЕФаЁе§ЗНаЮИіЪ§ЃЌЫљвд1ЃЋ3ЃЋ5ЃЋЁЃЋЃЈ2nЃ1ЃЉЃНn2ЃЛ
ЃЈ2ЃЉ(nЃЋ1)2Ѓn2БэЪОЕк(nЃЋ1)ИіЭМаЮБШЕкnИіЭМаЮЖрЕФаЁе§ЗНаЮИіЪ§ЃЌЫљвд(nЃЋ1)2Ѓn2ЃН2nЃЋ1ЃЎ
ЁОжЊЪЖдЫгУЁП
дЫгУвЛЃК
ЃЈ1ЃЉгЩвдЩЯПЩжЊ1ЃЋ3ЃЋ5ЃЋЁЃЋЃЈ2nЃ1ЃЉЃНn2ЃЌСюnЃН7ЃЌдђга72ЃН1ЃЋ3ЃЋ5ЃЋ7ЃЋ9ЃЋ11ЃЋ13ЃЛ
ЃЈ2ЃЉ99ЃН100Ѓ1
ЃН102Ѓ1
ЃН1ЃЋ3ЃЋ5ЃЋЁЃЋ19Ѓ1
ЃН3ЃЋ5ЃЋЁЃЋ19ЃЛ
Лђ99ЃН182Ѓ152
ЃН(1ЃЋ3ЃЋ5ЃЋЁЃЋ35)Ѓ(1ЃЋ3ЃЋ5ЃЋЁЃЋ29)
ЃН31ЃЋ33ЃЋ35ЃЛ
дЫгУЖўЃК
НЋдЪНУПСНЯюЗжЮЊвЛзщЃЌШЛКѓРћгУЧАУцЗЂЯжЕФЙцТЩ(nЃЋ1)2Ѓn2ЃН2nЃЋ1НјааНтД№МДПЩЃЎ
ЪдЬтНтЮіЃК
ЁОЮЪЬтЬНОПЁП
Ек(nЃЋ1)ИіЭМаЮБШЕкnИіЭМаЮЖр ЃЈ2nЃЋ1ЃЉ ИіаЁе§ЗНаЮЃЎ
ПЩЗЂЯжвдЯТНсТлЃКЃЈ1ЃЉ1ЃЋ3ЃЋ5ЃЋЁЃЋЃЈ2nЃ1ЃЉЃН n2 ЃЎ
ЃЈ2ЃЉ(nЃЋ1)2Ѓn2 ЃН 2nЃЋ1 ЃЎ
ЁОжЊЪЖдЫгУЁП
дЫгУвЛЃК
ЃЈ1ЃЉ72ЃН 1ЃЋ3ЃЋ5ЃЋ7ЃЋ9ЃЋ11ЃЋ13 ЃЎ
ЃЈ2ЃЉ99 ЃН 3ЃЋ5ЃЋ7ЃЋ9ЃЋ11ЃЋ13ЃЋ15ЃЋ17ЃЋ19 Лђ 31ЃЋ33ЃЋ35 ЃЎЃЈЬювЛжжМДПЩЃЉ
дЫгУЖўЃК
ЃЈЗЈвЛЃЉЃКдЪНЃНЃЈ22Ѓ1ЃЉЃЋ(42Ѓ32)ЃЋЃЈ62Ѓ52ЃЉЃЋЁЃЋЃЈ282Ѓ272ЃЉ
ЃНЃЈ2ЁС1ЃЋ1ЃЉЃЋЃЈ2ЁС3ЃЋ1ЃЉЃЋЃЈ2ЁС5ЃЋ1ЃЉЃЋЁЃЋЃЈ2ЁС27ЃЋ1ЃЉ
ЃН 2ЁСЃЈ1ЃЋ3ЃЋ5ЃЋЁЃЋ27ЃЉЃЋ14
ЃН 2ЁС196ЃЋ14
ЃН 406
ЃЈЗЈЖўЃЉЃКдЪНЃН ЃЈ22Ѓ1ЃЉЃЋ(42Ѓ32)ЃЋЃЈ62Ѓ52ЃЉЃЋЁЃЋЃЈ282Ѓ272ЃЉ
ЃН 1ЃЋ2ЃЋ3ЃЋ4ЃЋ5ЃЋ6ЃЋЁЃЋ27ЃЋ28
ЃН ![]()
ЃН 406



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПУЗПжжзгЙЋЫОвдвЛЖЈМлИёЯњЪлЁАЛЦН№1КХЁБгёУзжжзгЃЌШчЙћвЛДЮЙКТђ10ЧЇПЫвдЩЯЃЈВЛКЌ10ЧЇПЫЃЉЕФжжзгЃЌГЌЙ§10ЧЇПЫЕФФЧВПЗжжжзгЕФМлИёНЋДђелЃЌВЂвРДЫЕУЕНИЖПюН№ЖюyЃЈЕЅЮЛЃКдЊЃЉгывЛДЮЙКТђжжзгЪ§СПxЃЈЕЅЮЛЃКЧЇПЫЃЉжЎМфЕФКЏЪ§ЙиЯЕШчЭМЫљЪОЃЌЯТСаЫФжжЫЕЗЈЃК
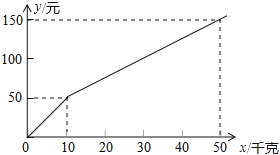
ЂйвЛДЮЙКТђжжзгЪ§СПВЛГЌЙ§10ЧЇПЫЪБЃЌЯњЪлМлИёЮЊ5дЊ/ЧЇПЫЃЛ
ЂквЛДЮЙКТђ30ЧЇПЫжжзгЪБЃЌИЖПюН№ЖюЮЊ100дЊЃЛ
ЂлвЛДЮЙКТђ10ЧЇПЫвдЩЯжжзгЪБЃЌГЌЙ§10ЧЇПЫЕФФЧВПЗжжжзгЕФМлИёДђЮхелЃЛ
ЂмвЛДЮЙКТђ40ЧЇПЫжжзгБШЗжСНДЮЙКТђЧвУПДЮЙКТђ20ЧЇПЫжжзгЩйЛЈ25дЊЧЎЃЎ
Цфжае§ШЗЕФИіЪ§ЪЧЃЈЁЁЁЁЃЉ
A. 1Иі B. 2Иі C. 3Иі D. 4Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаУќЬтжаЃЌЪЧецУќЬтЕФЪЧЃЈ ЃЉ
A. ЭЌЮЛНЧЯрЕШ B. ДЙжБгкЭЌвЛжБЯпЕФСНжБЯпЦНаа
C. ЯрЕШЕФНЧЪЧЖдЖЅНЧ D. ЦНаагкЭЌвЛжБЯпЕФСНжБЯпЦНаа
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЕчзгЬјдщгЮЯЗХЬЪЧШчЭМЫљЪОЕФЁїABCЃЌABЃН6ЃЌACЃН7ЃЌBCЃН8ЁЃШчЙћЬјдщПЊЪМЪБдкBCБпЕФP0ДІЃЌBP0ЃН2ЁЃЬјдщЕквЛВНДгP0ЬјЕНACБпЕФP1ЃЈЕк1ДЮТфЕуЃЉДІЃЌЧвCP1ЃНCP0ЃЛЕкЖўВНДгP1ЬјЕНABБпЕФP2ЃЈЕк2ДЮТфЕуЃЉДІЃЌЧвAP2ЃНAP1ЃЛЕкШ§ВНДгP2ЬјЕНBCБпЕФP3ЃЈЕк3ДЮТфЕуЃЉДІЃЌЧвBP3ЃНBP2ЃЛЁЁЃЛЬјдщАДЩЯЪіЙцдђвЛжБЬјЯТШЅЃЌЕкnДЮТфЕуЮЊPnЃЈnЮЊе§ећЪ§ЃЉЃЌдђЕуP2007гыP2010жЎМфЕФОрРыЮЊЃЈ ЃЉЁЃ
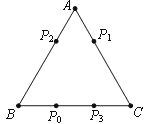
A. 1 B. 2 C. 3 D. 4
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕxOyжаЃЌжБЯпy=kx+4ЃЈkЁй0ЃЉгыyжсНЛгкЕуAЃЎ
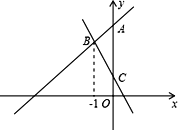
ЃЈ1ЃЉШчЭМЃЌжБЯпy=Љ2x+1гыжБЯпy=kx+4ЃЈkЁй0ЃЉНЛгкЕуBЃЌгыyжсНЛгкЕуCЃЌЕуBЕФКсзјБъЮЊЃ1ЃЎ
ЂйЧѓЕуBЕФзјБъМАkЕФжЕЃЛ
ЂкжБЯпy=Љ2x+1гыжБЯпy=kx+4гыyжсЫљЮЇГЩЕФЁїABCЕФУцЛ§ЕШгк ЃЛ
ЃЈ2ЃЉжБЯпy=kx+4ЃЈkЁй0ЃЉгыxжсНЛгкЕуEЃЈx 0 ЃЌ0ЃЉЃЌШєЉ2ЃМx 0 ЃМЉ1ЃЌЧѓkЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
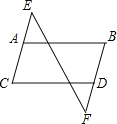
ЁОЬтФПЁПШчЭМЃЌЯжгавдЯТ3ОфЛАЃКЂйABЁЮCDЃЌЂкЁЯB=ЁЯCЃЎЂлЁЯE=ЁЯFЃЎЧывдЦфжа2ОфЛАЮЊЬѕМўЃЌЕкШ§ОфЛАЮЊНсТлЙЙдьУќЬтЃЎР§ШчЃКгЩЂйЂкЕУЂлЃЎ
ЃЈ1ЃЉФуЛЙФмЙЙдьМИИіУќЬтЃПЧыЗТееЩЯУцЕФР§згЃЌНЋЫќУЧаДГіРДЃЎ
ЃЈ2ЃЉФуЙЙЫљдьЕФУќЬтЪЧецУќЬтЛЙЪЧМйУќЬтЃПЧыбЁдёвЛИіМгвджЄУїЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
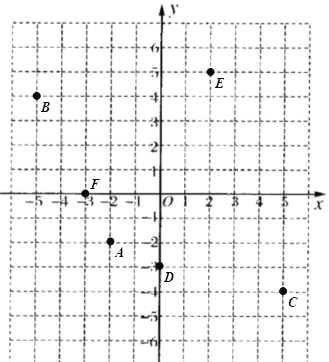
ЁОЬтФПЁПЃЈ1ЃЉаДГіЭМжаЕуAЁЂBЁЂCЁЂDЁЂEЁЂFЕФзјБъЃЎ
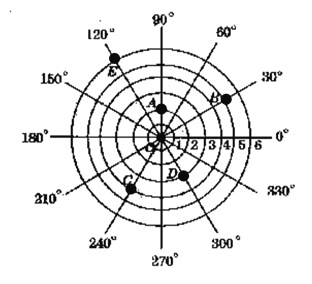
ЃЈ2ЃЉШчЭМЪЧвЛЬЈРзДяЬНВтЯрЙиФПБъЕУЕНЕФНсЙћЃЌШєМЧЭМжаФПБъAЕФЮЛжУЮЊЃЈ2ЃЌ90ЁуЃЉЃЌдђЦфгрИїФПБъЕФЮЛжУЗжБ№ЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com