
����Ŀ��÷�����ӹ�˾��һ���۸��������ƽ�1�����������ӣ����һ�ι���10ǧ�����ϣ�����10ǧ�ˣ������ӣ�����10ǧ�˵��Dz������ӵļ۸��ۣ������˵õ�������y����λ��Ԫ����һ�ι�����������x����λ��ǧ�ˣ�֮��ĺ�����ϵ��ͼ��ʾ����������˵����
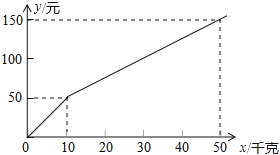
��һ�ι�����������������10ǧ��ʱ�����ۼ۸�Ϊ5Ԫ/ǧ�ˣ�
��һ�ι���30ǧ������ʱ��������Ϊ100Ԫ��
��һ�ι���10ǧ����������ʱ������10ǧ�˵��Dz������ӵļ۸�����ۣ�
��һ�ι���40ǧ�����ӱȷ����ι�����ÿ�ι���20ǧ�������ٻ�25ԪǮ��
������ȷ�ĸ����ǣ�������
A. 1�� B. 2�� C. 3�� D. 4��
���𰸡�D
������������ͼ��֪������10ǧ��������Ҫ50Ԫ���ɴ����һ�ι�����������������10ǧ��ʱ�����ۼ۸�
����ͼ��֪������10ǧ���Ժ������Dz������ӵĵ��۽��ͣ����ɹ���50ǧ�˱ȹ���10ǧ�����Ӷึ100Ԫ���������10ǧ���Ժ������Dz������ӵĵ��ۣ��ټ����һ�ι���30ǧ������ʱ�ĸ����
������һ�ι���10ǧ����������ʱ������10ǧ�˵��Dz������ӵļ۸�Ϊ2.5Ԫ/ǧ�ˣ���2.5��5=0.5�����Կ���������������
�������һ�ι���40ǧ�����ӵĸ�����Ϊ125Ԫ������������ι�����ÿ�ι���20ǧ�����ӵĸ�����Ϊ150Ԫ��Ȼ����150��ȥ125���������һ�ι���40ǧ�����ӱȷ����ι�����ÿ�ι���20ǧ�������ٻ���Ǯ����
�⣺����ͼ��֪��һ�ι�����������������10ǧ��ʱ�����ۼ۸�Ϊ��50��10=5Ԫ/ǧ�ˣ���ȷ��
����ͼ��֪������10ǧ�˵��Dz������ӵļ۸�Ϊ����150-50������50-10��=2.5Ԫ/ǧ�ˣ����ԣ�һ�ι���30ǧ������ʱ��������Ϊ��50+2.5����30-10��=100Ԫ����ȷ��
������һ�ι���10ǧ����������ʱ������10ǧ�˵��Dz������ӵļ۸�Ϊ2.5Ԫ/ǧ�ˣ���2.5��5=0.5�����Դ����ۣ���ȷ��
������һ�ι���40ǧ��������Ҫ��50+2.5����40-10��=125Ԫ��
�����ι�����ÿ�ι���20ǧ��������Ҫ��2��[50+2.5����20-10��]=150Ԫ��
��150-125=25Ԫ��
����һ�ι���40ǧ�����ӱȷ����ι�����ÿ�ι���20ǧ�������ٻ�25ԪǮ����ȷ��
��ѡD��


 �ƸԴ��ž�ϵ�д�
�ƸԴ��ž�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����м�����ȷ���ǣ� ��
A.7a+a=7a2
B.5y��3y=2
C.3x2y��2yx2=x2y
D.3a+2b=5ab
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ÿһ�������е�������ֵ�ֱ�Ϊ�����ε����߳������ܹ���ֱ�������ε��ǣ�������
A.3��4��5B.6��8��10C.5��12��13D.5��5��7
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ż�ʱ��С��һ������һ���С�γ�ȥ����̽��үү�����̺�������š����ϴӼ��������������6ǧ������������Ȼ����������1.5ǧ��үү�ң������үү�ҳ�����������12ǧ����ң����Ϸ��ؼ��
��1�����Լ�Ϊԭ�㣬��Ϊ��������1����λ���ȱ�ʾ1ǧ�ף��뽫���С�үү�Һ���ҵ�λ�������������Ϸֱ��õ�A��B��C��ʾ������
![]()
��2���ʳ���A�����C������ǧ�ף�
��3����С�γ�ÿǧ����0.08������С��һ�Ҵӳ��������ؼ�������·��С���ĺ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Բ����������Ϊ18cm�������ܳ�Ϊ24cm���ڱ��ڱ��뱭��4cm�ĵ�B����һ�η��ۣ���ʱһֻ���������ڱ���ڣ��뱭����2cm�������Եĵ�A����Ϊ�˳Ե����ۣ����ϴ����A���������·�������ڱ�B����
��1����ͼ�DZ��ӵIJ���չ��ͼ�����ڱ���CD��ȷ��һ��P,ʹ������A-P-B·�����У�������̡�
��2�������ͼ������������е����·������
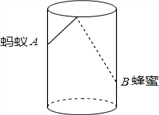
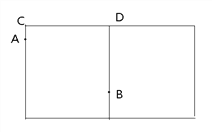
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ������ε�ÿһ����Ƕ����������ڵ��ڽǵ�һ�룬���������εı����ǣ� ��
A.3B.4C.5D.6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ķ����������һ������С���ĸ���λ�ϵ����֣���С�����ֵ�ijһλ�𣬰�һ��˳���ظ����֣���ô������С����������ѭ��С�������ѭ��С�������磬0.333����д��![]() ����������ѭ��С����Ϊ��ѭ��С�������磬0.1666����0.0456456456�������ǿɷֱ�д��
����������ѭ��С����Ϊ��ѭ��С�������磬0.1666����0.0456456456�������ǿɷֱ�д��![]() ��
��![]() ����������ѭ��С����Ϊ��ѭ��С����
����������ѭ��С����Ϊ��ѭ��С����
������̽����
С���κ����÷��̵�֪ʶ̽�����֣����д�ѭ��С�������Ի�Ϊ���������磬��![]() Ϊ��������������ǣ���
Ϊ��������������ǣ���![]() =
=![]() ����
����![]() =0.333�������������߶�
=0.333�������������߶�![]() 10����10
10����10![]() =3.333������10
=3.333������10![]() =3+0.333��������Ϊ
=3+0.333��������Ϊ![]() =0.333��������10
=0.333��������10![]() =3+
=3+![]() ������9
������9![]() =3����
=3����![]() =
=![]() ������
������![]() =
=![]() ��
��
���Խ�����и��⣺
��1����![]() ���ɷ���Ϊ___________��
���ɷ���Ϊ___________��
��2��������С���ķ������Ѵ�ѭ��С��![]() ���ɷ�����
���ɷ�����
�����������
ѭ��С�����ظ����ֵ�һ�������ֽ�������һ��ѭ���ڣ�����0.333����0.0456456456����ѭ���ڷֱ�Ϊ��3������456������ʵ���Ѵ�ѭ��С����Ϊ����ʱ�������ķ���������һ��ѭ���ڵ���������ɵ�������ĸ�������ɸ�9��ɣ�9�ĸ���Ϊһ��ѭ���ڵ����ֵĸ��������磺![]() ��
��![]() ��
��![]() ��
��
��ֱ��д�����´�ѭ��С����Ϊ�����Ľ����![]() =____________��
=____________��![]() =____________��
=____________��
��������չ��
С���ڶԻ�ѭ��С���о�ʱ���֣����л�ѭ��С���������Ȼ�Ϊ��ѭ��С����Ȼ���ٻ�Ϊ���������磺![]() ��
��
��ѻ�ѭ��С��![]() ��Ϊ������
��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������̽������ͬ����С��С������ֽƬ������ͼ�ķ�ʽƴ��������
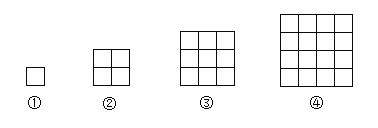
���ɣ��ڢٸ�ͼ������1��С�����Σ�
�ڢڸ�ͼ�αȵڢٸ�ͼ�ζ�3��С�����Σ�
�ڢ۸�ͼ�αȵڢڸ�ͼ�ζ�5��С�����Σ�
����
��(n+1)��ͼ�αȵ�n��ͼ�ζ�________��С��������
�ɷ������½��ۣ���1��1+3+5+��+��2n��1��= ____________��
��2��(n+1)2��n2 = ____________��
��֪ʶ���á�
����һ�����һ�������ü�������������������ʾ�����dz������Ϊ�������������磺9=1+3+5��32=5+7+9+11�����9��32���ǡ���������
�볢�Խ����С������������������ĺͱ�ʾ������
��1��![]() =_____________________________________��
=_____________________________________��
��2��99 =_____________________________________��
���ö�����������Ľ��ۣ������![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com