【题目】下列命题中，是真命题的是（ ）
A. 同位角相等 B. 垂直于同一直线的两直线平行
C. 相等的角是对顶角 D. 平行于同一直线的两直线平行
科目：初中数学 来源： 题型：
【题目】【阅读理解】如果一个无限小数的各数位上的数字，从小数部分的某一位起，按一定顺序不断重复出现，那么这样的小数叫做无限循环小数，简称循环小数．例如，0.333…，写作
，像这样的循环小数称为纯循环小数．又如，0.1666…、0.0456456456…，它们可分别写作
、
，像这样的循环小数称为混循环小数．
【问题探究】
小明课后利用方程的知识探索发现，所有纯循环小数都可以化为分数，例如，化为分数，解决方法是：设
=，即=0.333…，将方程两边都
10，得10=3.333…，即10=3+0.333…，又因为=0.333…，所以10=3+，所以9=3，即=
，所以=．
尝试解决下列各题：
（1）把
化成分数为___________．
（2）请利用小明的方法，把纯循环小数
化成分数．
【问题归纳】
循环小数中重复出现的一个或几个数字叫做它的一个循环节，例如0.333…、0.0456456456…的循环节分别为“3”、“456”．其实，把纯循环小数化为分数时，分数的分子是它的一个循环节的数字所组成的数，分母则由若干个9组成，9的个数为一个循环节的数字的个数．例如：
；
；
．
请直接写出以下纯循环小数化为分数的结果：
=____________，
=____________．
【问题拓展】
小丽在对混循环小数研究时发现，所有混循环小数都可以先化为纯循环小数，然后再化为分数．例如：
．
请把混循环小数
化为分数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某一出租车一天下午以鼓楼为出发地在东西方向营运，向东为正，向西为负，行车里程（单位：km）依先后次序记录如下：+2、 
、 
、 +4、 、 +6、 
、。
（1）将最后一名乘客送到目的地，出租车离鼓楼出发点多远？在鼓楼的什么方向？
（2）若每千米的价格为2.4元，司机一个下午的营业额是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】【问题探究】用同样大小的小正方形纸片，按下图的方式拼正方形．
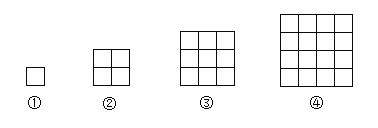
规律：第①个图形中有1个小正方形；
第②个图形比第①个图形多3个小正方形；
第③个图形比第②个图形多5个小正方形；
……
第(n+1)个图形比第n个图形多________个小正方形．
可发现以下结论：（1）1+3+5+…+（2n－1）= ____________．
（2）(n+1)2－n2 = ____________．
【知识运用】
运用一：如果一个数可用几个连续的奇数和来表示，我们称这个数为“好数”，例如：9=1+3+5，32=5+7+9+11，则称9和32都是“好数”．
请尝试将下列“好数”用连续奇数的和表示出来：
（1）
=_____________________________________．
（2）99 =_____________________________________．
运用二：利用上面的结论，请计算
的值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
