
ѧ�ꡰ��Գơ���һ�º���ʦ������һ��˼���⣺��ͼ��ʾ����M��N�ֱ��ڵȱߡ�ABC��BC��CA���ϣ���BM=CN��AM��BN���ڵ�Q����֤����BQM=60�㣮

��1������������˼���⣺
��2�����꣨1����ͬѧ������ʦ�������½����˷�˼������������⣬�磺
���������С�BM=CN���롰��BQM=60�㡱��λ�ý������õ����Ƿ����������⣿
���������еĵ�M��N�ֱ��ƶ���BC��CA���ӳ����ϣ��Ƿ����ܵõ���BQM=60 ��
��
���������е���������M��N�ֱ�����������ABC��BC��CA���ϡ���Ϊ����M��N�ֱ���������ABCD��BC��CD���ϡ����Ƿ����ܵõ���BQM=60�㣿����
���������жϣ������к�������д���ǡ���
��________����_______����________�����Ԣڣ��۵��жϣ�ѡ��һ������ͼ�Σ�������֤����
��1��֤���������������2���� �� �� �� �� ��֤�������������
��������
�����������1����������ABCΪ�ȱ������Σ����õȱ������ε����ʵõ���������ȣ���������ȣ�����SAS�õ�������ABM��������BCNȫ�ȣ�����ȫ�������εĶ�Ӧ����ȵõ�һ�Խ���ȣ�����������ʼ������������ɵ�֤��
��2�����������⣬��������۽��������������Խ���ȵ����������Ƶõ�������BMQ��������ABM���ƣ��������������εĶ�Ӧ����ȵõ�һ�Խ���ȣ�����ASA�õ�������ABM��������BCNȫ�ȣ�����ȫ�������ζ�Ӧ����ȼ��ɵ�֤�����������⣬������ǵ����ʵõ��н���ȣ�����SAS�õ�������ACM��������ABNȫ�ȣ�����ȫ�������εĶ�Ӧ����ȵõ�һ�Խ���ȣ����õ�ʽ�����ʱ��μ��ɵ�֤���۲��������⣬����HL�õ�ֱ��������ABM��������BCNȫ�ȣ�����ȫ�������ζ�Ӧ����ȵõ���AMB=��BNC������ֱ��������BNC������ǻ��࣬���õ�����������ֱ�Ķ����жϵõ���BQM=90�㣮
�����������1���ߡ�ABCΪ�ȱ������Σ���AB=BC=AC����BAC=��ABC=��ACB=60�㣬
�ڡ�ABM�͡�BCN�У���BM=CN����ABM=��BCN��AB=BC�����ABM�ա�BCN��SAS����
���BAM=��CBN�����BQM=��BAQ+��ABQ=��MBQ+��ABQ=60�㣻
��2�����ǣ����ǣ��۷�
��ѡ��٣���֪����BQM=60�㣬
��֤��BM=CN��
֤�����ߡ�BQM=��ABM=60�㣬��BMQ=��AMB�����BMQ�ס�AMB�����CBN=��BAM��
�ڡ�ABM�͡�BCN�У��ߡ�BAM=��CBN��AB=BC����ABM=��BCN�����ABM�ա�BCN��ASA����
��BM=CN��
��ѡ��ڣ�֤������ͼ��
�ڡ�ACM�͡�BAN�У���CM=AN����ACM=��BAN=120�㣬AC=AB�����ACM�ա�BAN��SAS����
���AMC=��BNA�����NQA=��NBC+��BMQ=��NBC+��BNA=180�㩁60��=120�㣬���BQM=60�㣻
��ѡ��ۣ�֤������ͼ��
��Rt��ABM��Rt��BCN����BM=CN��AB=BC����Rt��ABM��Rt��BCN��HL�������AMB=��BNC��
�֡ߡ�NBM+��BNC=90�㣬���QBM+��QMB=90�㣬���BQM=90�㣮
�ʴ�Ϊ�����ǣ����ǣ��۷�
���㣺1��ȫ�������ε��ж������ʣ�2���ȱ������ε����ʣ�


 ��У���˿��ֿ���ϵ�д�
��У���˿��ֿ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2014-2015ѧ�긣��ʡ��������ѧУ���꼶��ѧ�����п�����ѧ�Ծ��������棩 ���ͣ������
��ͼ����ABC�У���C=90�㣬 ,��ABC�����Ϊ7����AB= .
,��ABC�����Ϊ7����AB= .

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�긣��ʡ���������꼶��ѧ�ڰ��ڿ�����ѧ�Ծ��������棩 ���ͣ������
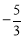 �ĵ����ľ���ֵ�� ��
�ĵ����ľ���ֵ�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ��������ʯ��ˮԴ��������꼶��ѧ����ĩģ����ѧ�Ծ��������棩 ���ͣ������
 ��
�� ��ͬ�����a+b��ֵ��________.
��ͬ�����a+b��ֵ��________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ��������ʯ��ˮԴ��������꼶��ѧ����ĩģ����ѧ�Ծ��������棩 ���ͣ�ѡ����
����ʽ����ȷ���ǣ� ��
A.
B.
C.
D.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�긣��ʡ�����а��꼶��ѧ�ڰ��ڿ�����ѧ�Ծ��������棩 ���ͣ������
��ͼ����֪��ACB=��ADB=90�㣬AC=AD��E��AB�ϣ�����CE��DE.

��1�������ҳ����E�йص�����ȫ�ȵ������Σ�
��2��ѡ��1���е�һ��ȫ�������μ���֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�긣��ʡ�����а��꼶��ѧ�ڰ��ڿ�����ѧ�Ծ��������棩 ���ͣ�ѡ����
��ͼ���ڡ�AOB�������Ͻ�ȡAO=BO ��OC=OD������AD��BC���ڵ�P������OP����ͼ��ȫ�������ι��У� ���ԣ�

A��2 B��3 C��4 D��5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ��������ʯ��ˮԴ��������꼶��ѧ����ĩģ����ѧ�Ծ��������棩 ���ͣ������
��8�֣��������ϣ�ij��ѧ�����꼶�����������������ϲ��ԣ�������7��Ϊ�����ڱ��Ĵ�
����Ϊ����������Ĵ�����Ϊ����������8�������ijɼ�Ϊ+2��-1��+3��0��-2��-3��+1��0.
��1����8�������дﵽ����ռ�ٷ�֮����
��2�����ǹ����˶��ٴ��������ϣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ������ʡ���������꼶��ѧ�����п�����ѧ�Ծ��������棩 ���ͣ������
�� ��
�� �������ϵ�λ����ͼ��ʾ��
�������ϵ�λ����ͼ��ʾ��

����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com