
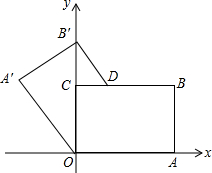
 如图,矩形OABC的顶点O是坐标原点,顶点A、C分别在x轴、y轴的正半轴上,顶点B在第一象限,OA=8,OC=6,点D在边BC上,将四边形OABD沿直线OD翻折,使点A和点B分别落在这个坐标平面的点A′和点B′处,且点B′刚好落在y轴上.若某反比例函数的图象经过点A′,则这个反比例函数的解析式为
如图,矩形OABC的顶点O是坐标原点,顶点A、C分别在x轴、y轴的正半轴上,顶点B在第一象限,OA=8,OC=6,点D在边BC上,将四边形OABD沿直线OD翻折,使点A和点B分别落在这个坐标平面的点A′和点B′处,且点B′刚好落在y轴上.若某反比例函数的图象经过点A′,则这个反比例函数的解析式为| 24 |
| 5 |
| 32 |
| 5 |
| 24 |
| 5 |
| 32 |
| 5 |
| k |
| x |
 解:作A′E⊥y轴于E,连接OB,如图,
解:作A′E⊥y轴于E,连接OB,如图,| OA2+AB2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 6×8 |
| 10 |
| 24 |
| 5 |
| OA′2-A′E2 |
| 32 |
| 5 |
| 24 |
| 5 |
| 32 |
| 5 |
| k |
| x |
| 24 |
| 5 |
| 32 |
| 5 |
| 768 |
| 25 |
| 768 |
| 25x |
| 768 |
| 25x |


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:初中数学 来源: 题型:
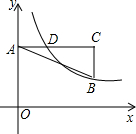 如图,在直角坐标系中,点A在y轴正半轴上,AC∥x轴,点B,C的横坐标都是3,且BC=2,点D在AC上,且横坐标为1,若反比例函数y=
如图,在直角坐标系中,点A在y轴正半轴上,AC∥x轴,点B,C的横坐标都是3,且BC=2,点D在AC上,且横坐标为1,若反比例函数y=| k |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、了解我市所有居民的年收入 |
| B、了解我市居民的环保意识 |
| C、了解我市每天进出的人数 |
| D、了解你校数学教师的年龄状况 |
查看答案和解析>>
科目:初中数学 来源: 题型:
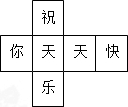 一个材质均匀的正方体的六个面上分别标有文字“祝、你、天、天、快、乐”,其表面展开图如图.随机抛掷这个正方体,结果“天”字朝上的概率是( )
一个材质均匀的正方体的六个面上分别标有文字“祝、你、天、天、快、乐”,其表面展开图如图.随机抛掷这个正方体,结果“天”字朝上的概率是( )A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、(2a+b)(2b-a) |
| B、(x+1)(-x-1) |
| C、(-m-n)(-m+n) |
| D、(3x-y)(-3x+y) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com