
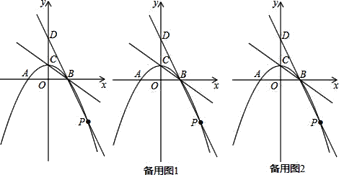
ЁОЬтФПЁПШчЭМ1ЃЌдкЁїABCжаЃЌABЃНACЃЌЕуDЪЧBCБпЩЯвЛЕуЃЈВЛгыЕуBЃЌCжиКЯЃЉЃЌвдADЮЊБпдкADЕФгвВрзїЁїADEЃЌЪЙADЃНAEЃЌЁЯDAEЃНЁЯBACЃЌСЌНгCEЃЎЩшЁЯBACЃНІСЃЌЁЯBCEЃНІТЃЎ
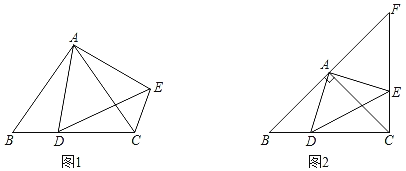
ЃЈ1ЃЉЧѓжЄЃКЁїCAEЁеЁїBADЃЛ
ЃЈ2ЃЉЬНОПЃКЕБЕуDдкBCБпЩЯвЦЖЏЪБЃЌІСЁЂІТжЎМфгадѕбљЕФЪ§СПЙиЯЕЃПЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌШєЁЯBACЃН90ЁуЃЌCEгыBAЕФбгГЄЯпНЛгкЕуFЃЎЧѓжЄЃКEFЃНDCЃЎ
ЁОД№АИЁПЃЈ1ЃЉЯъМћНтЮіЃЛЃЈ2ЃЉІС+ІТЃН180ЁуЃЛРэгЩМћНтЮіЃЛЃЈ3ЃЉЯъМћНтЮіЃЛ
ЁОНтЮіЁП
ЃЈ1ЃЉЪзЯШгЩЁЯDAEЃНЁЯBACЃЌЕУГіЁЯCAEЃНЁЯBADЃЌШЛКѓгЩADЃНAEЃЌACЃНABЃЌМДПЩХаЖЈЁїCAEЁеЁїBADЃЛ
ЃЈ2ЃЉЪзЯШгЩЁїCAEЁеЁїBADЃЌЕУГіЁЯACEЃНЁЯBЃЌШЛКѓгЩABЃНACЃЌЕУГіЁЯBЃНЁЯACBЃЌНјЖјЕУГіЁЯACEЃНЁЯBЃНЁЯACBЃЌЁЯBCEЃНІТЃН2ЁЯBЃЌМДПЩЕУГіІС+ІТЃН180ЁуЃЛ
ЃЈ3ЃЉгЩЁїCAEЁеЁїBADЃЌЕУГіCEЃНBDЃЌдйгЩЁЯBACЃН90ЁуЃЌABЃНACЃЌЕУГіЁЯBЃНЁЯACBЃН45ЁуЃЌгжгЩЁЯBCF+ЁЯBACЃН180ЁуЃЌЕУГіЁЯBCFЃН90ЁуЃЌЁЯFЃНЁЯBЃН45ЁуЃЌНјЖјЕУГіCFЃНCBЃЌМДПЩЕУГіEFЃНDCЃЎ
ЃЈ1ЃЉжЄУїЃКЁпЁЯDAEЃНЁЯBACЃЌ
ЁрЁЯDAEЉЁЯDACЃНЁЯBACЉЁЯDACЃЌ
ЁрЁЯCAEЃНЁЯBADЃЎ
ЁпADЃНAEЃЌACЃНABЃЌ
ЁрЁїCAEЁеЁїBADЃЈSASЃЉЃЎ
ЃЈ2ЃЉНтЃКІС+ІТЃН180ЁуЃЌ
РэгЩШчЯТЃК
гЩЁїCAEЁеЁїBADЃЌ
ЁрЁЯACEЃНЁЯBЃЎ
ЁпABЃНACЃЌ
ЁрЁЯBЃНЁЯACBЃЎ
ЁрЁЯACEЃНЁЯBЃНЁЯACBЃЎ
ЁрЁЯBCEЃНІТЃН2ЁЯBЃЌ
дкЁїABCжаЃЌЁЯBACЃНІСЃН180ЁуЉ2ЁЯBЃЎ
ЁрІС+ІТЃН180ЁуЃЎ
ЃЈ3ЃЉжЄУїЃКгЩЃЈ1ЃЉжЊЃЌЁїCAEЁеЁїBADЃЌ
ЁрCEЃНBDЃЎ
ЁпЁЯBACЃН90ЁуЃЌABЃНACЃЌ
ЁрЁЯBЃНЁЯACBЃН45ЁуЃЌ
гЩЃЈ2ЃЉЕУЃЌЁЯBCF+ЁЯBACЃН180ЁуЃЎ
ЁрЁЯBCFЃН90ЁуЃЎ
ЁрЁЯFЃНЁЯBЃН45ЁуЃЌ
ЁрCFЃНCBЃЎ
ЁрCFЉCEЃНCBЉBDЃЎ
ЁрEFЃНDCЃЎ


 ЧЇРяТэзпЯђМйЦкЦкФЉЗТецЪдОэКЎМйЯЕСаД№АИ
ЧЇРяТэзпЯђМйЦкЦкФЉЗТецЪдОэКЎМйЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁїABCжаЃЌAB=ACЃЌADЪЧЁїABCЕФНЧЦНЗжЯпЃЌЕуOЮЊABЕФжаЕуЃЌСЌНгDOВЂбгГЄЕНЕуEЃЌЪЙOE=ODЃЌСЌНгAEЃЌBEЃЎ

ЃЈ1ЃЉЧѓжЄЃКЫФБпаЮAEBDЪЧОиаЮЃЛ
ЃЈ2ЃЉЕБЁїABCТњзуЪВУДЬѕМўЪБЃЌОиаЮAEBDЪЧе§ЗНаЮЃЌВЂЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌBDЪЧЕШБпШ§НЧаЮABCЕФНЧЦНЗжЯпЃЌEЪЧBCбгГЄЯпЩЯЕФвЛЕуЃЌЧвCE=CDЃЌDF=BCЃЌДЙзуЮЊFЃЎBFгыEFЯрЕШТ№ЃПЮЊЪВУДЃП

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁїABCжаЃЌABЕФДЙжБЦНЗжЯпЗжБ№НЛABЃЌBCгкDЃЌEЃЌACЕФДЙжБЦНЗжЯпЗжБ№НЛACЃЌBCгкFЃЌGЃЎ
ЃЈ1ЃЉШєЁїAEGЕФжмГЄЮЊ10ЃЌЧѓЯпЖЮBCЕФГЄЃЎ
ЃЈ2ЃЉШєЁЯBAC=128ЁуЃЌЧѓЁЯEAGЕФЖШЪ§ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
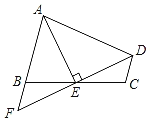
ЁОЬтФПЁПШчЭМЃЌдкЫФБпаЮABCDжаЃЌABЁЮDCЃЌEЮЊBCЕФжаЕуЃЌСЌНгDEЁЂAEЃЌAEЁЭDEЃЌбгГЄDEНЛABЕФбгГЄЯпгкЕуFЃЎШєABЃН5ЃЌCDЃН3ЃЌдђADЕФГЄЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ10ЗжЃЉЫЎЙћЕъеХАЂвЬвдУПНя2дЊЕФМлИёЙКНјФГжжЫЎЙћШєИЩНяЃЌШЛКѓвдУПНя4дЊЕФМлИёГіЪлЃЌУПЬьПЩЪлГі100НяЃЌЭЈЙ§ЕїВщЗЂЯжЃЌетжжЫЎЙћУПНяЕФЪлМлУПНЕЕЭ0.1дЊЃЌУПЬьПЩЖрЪлГі20НяЃЌЮЊБЃжЄУПЬьжСЩйЪлГі260НяЃЌеХАЂвЬОіЖЈНЕМлЯњЪлЃЎ
ЃЈ1ЃЉШєНЋетжжЫЎЙћУПНяЕФЪлМлНЕЕЭxдЊЃЌдђУПЬьЕФЯњЪлСПЪЧ НяЃЈгУКЌxЕФДњЪ§ЪНБэЪОЃЉЃЛ
ЃЈ2ЃЉЯњЪлетжжЫЎЙћвЊЯыУПЬьгЏРћ300дЊЃЌеХАЂвЬашНЋУПНяЕФЪлМлНЕЕЭЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
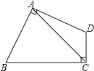
ЁОЬтФПЁПШчЭМЃЌдкЫФБпаЮ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌШчЙћ
ЃЌШчЙћ![]() ЃЌдђЫФБпаЮ
ЃЌдђЫФБпаЮ![]() ЕФУцЛ§ЮЊ________
ЕФУцЛ§ЮЊ________![]() ЃЎ
ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
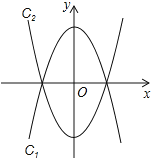
ЁОЬтФПЁПНЋХзЮяЯпc1ЃК ![]() биxжсЗелЃЌЕУЕНХзЮяЯпc2ЃЌШчЭМ1ЫљЪОЃЎ
биxжсЗелЃЌЕУЕНХзЮяЯпc2ЃЌШчЭМ1ЫљЪОЃЎ
(1)ЧыжБНгаДГіХзЮяЯпc2ЕФБэДяЪНЃЛ
(2)ЯжНЋХзЮяЯпc1ЯђзѓЦНвЦmИіЕЅЮЛГЄЖШЃЌЦНвЦКѓЕУЕНаТХзЮяЯпЕФЖЅЕуЮЊMЃЌгыxжсЕФНЛЕуДгзѓЕНгввРДЮЮЊAЁЂBЃЛНЋХзЮяЯпc2ЯђгввВЦНвЦmИіЕЅЮЛГЄЖШЃЌЦНвЦКѓЕУЕНаТХзЮяЯпЕФЖЅЕуЮЊNЃЌгы![]() жсЕФНЛЕуДгзѓЕНгввРДЮЮЊDЁЂEЃЎ
жсЕФНЛЕуДгзѓЕНгввРДЮЮЊDЁЂEЃЎ
ЂйЕБBЁЂDЪЧЯпЖЮAEЕФШ§ЕШЗжЕуЪБЃЌЧѓmЕФжЕЃЛ
ЂкдкЦНвЦЙ§ГЬжаЃЌЪЧЗёДцдквдЕуAЁЂNЁЂEЁЂMЮЊЖЅЕуЕФЫФБпаЮЪЧОиаЮЕФЧщаЮЃПШєДцдкЃЌЧыЧѓГіДЫЪБmЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌХзЮяЯпгы
жаЃЌХзЮяЯпгы![]() жсНЛгк
жсНЛгк![]() ЃЌ
ЃЌ![]() СНЕуЃЈЕу
СНЕуЃЈЕу![]() дкЕу
дкЕу![]() ЕФзѓВрЃЉЃЌЖЅЕуЮЊ
ЕФзѓВрЃЉЃЌЖЅЕуЮЊ![]() ЃЎжБЯп
ЃЎжБЯп![]() НЛ
НЛ![]() жсгкЕу
жсгкЕу![]() ЃЌНЛХзЮяЯпгкЕу
ЃЌНЛХзЮяЯпгкЕу![]() ЃЎ
ЃЎ
![]() ЧѓХзЮяЯпЕФБэДяЪНМАЕу
ЧѓХзЮяЯпЕФБэДяЪНМАЕу![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
![]() Еу
Еу![]() ЪЧХзЮяЯпЩЯЕФЖЏЕуЃЌШєвд
ЪЧХзЮяЯпЩЯЕФЖЏЕуЃЌШєвд![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЮЊЖЅЕуЕФЫФБпаЮНігавЛзщЖдБпЦНааЃЌЧѓЕу
ЮЊЖЅЕуЕФЫФБпаЮНігавЛзщЖдБпЦНааЃЌЧѓЕу![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
![]() СЌНг
СЌНг![]() ЃЌЕу
ЃЌЕу![]() дкжБЯп
дкжБЯп![]() ЩЯЃЌЩшЕу
ЩЯЃЌЩшЕу![]() ЕНжБЯп
ЕНжБЯп![]() ЕФОрРыЮЊ
ЕФОрРыЮЊ![]() ЃЌЕу
ЃЌЕу![]() ЕНЕу
ЕНЕу![]() ЕФОрРыЮЊ
ЕФОрРыЮЊ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФзюаЁжЕЃЎ
ЕФзюаЁжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com