
【题目】已知:如图①,在ABCD中,O为对角线BD的中点.过O的直线MN交直线AB于点M,交直线CD于点N;过O的另一条直线PQ交直线AD于点P,交直线BC于点Q,连接PN、MQ.
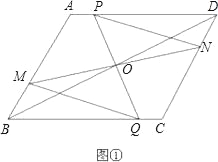

(1)试证明△PON与△QOM全等;
(2)若点O为直线BD上任意一点,其他条件不变,则△PON与△QOM又有怎样的关系?试就点O在图②所示的位置,画出图形,证明你的猜想;
(3)若点O为直线BD上任意一点(不与点B、D重合),设OD:OB=k,PN=x,MQ=y,则y与x之间的函数关系式为 .
【答案】(1)证明见解析;(2)证明见解析;(3)见解析.
【解析】
(1)根据平行四边形的性质容易得到全等条件证明△DOP≌△BOQ,△PON≌△QOM,然后利用全等三角形的性质得到PO=QO,MO=NO,然后再证明△PON≌△QOM就可以解决问题;
(2)点O为直线BD上任意一点,则△MOQ∽△NOP.根据AP∥BQ,BM∥CN可以得到比例线段,而∠NOP=∠MOQ,可以证明△MOQ∽△NOP了;
(3)根据(2)和已知可以得到![]() =
=![]() =
=![]() ,根据这个等式可以求出y与x之间的函数关系式.
,根据这个等式可以求出y与x之间的函数关系式.
(1)证明:在平行四边形ABCD中,AD∥BC,
∴∠PDO=∠QBO.
∵∠DOP=∠BOQ,DO=BO,
∴△DOP≌△BOQ.
∴PO=QO.
同理MO=NO.
∵∠PON=∠QOM,
∴△PON≌△QOM.
(2)解:画图如图所示.
△MOQ∽△NOP.
∵AP∥BQ,BM∥CN,
∴OD:OB=OP:OQ,OD:OB=ON:OM.
∴OP:OQ=ON:OM.
∴∠NOP=∠MOQ.
∴△MOQ∽△NOP.
(3)解:根据(2)和已知可以得到![]() =
=![]() =
=![]() ,
,
∵OD:OB=k,PN=x,MQ=y,
∴y=![]() .
.


科目:初中数学 来源: 题型:
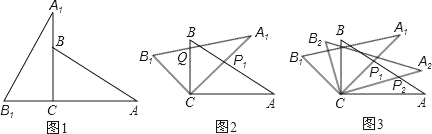
【题目】将两块全等的三角板如图1摆放,其中∠A1CB1=∠ACB=90°,∠A1=∠A=30°.
(1)将图1中△A1B1C绕点C顺时针旋转45°得图2,点P1是A1C与AB的交点,点Q是A1B1与BC的交点,求证:CP1=CQ;
(2)在图2中,若AP1=a,则CQ等于多少?
(3)将图2中△A1B1C绕点C顺时针旋转到△A2B2C(如图3),点P2是A2C与AP1的交点.当旋转角为多少度时,有△AP1C∽△CP1P2?这时线段CP1与P1P2之间存在一个怎样的数量关系?.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】几何体的三视图相互关联.已知直三棱柱的三视图如图,在△PMN中,∠MPN=90°,PN=4,sin∠PMN=![]() .
.
(1)求BC及FG的长;
(2)若主视图与左视图两矩形相似,求AB的长;
(3)在(2)的情况下,求直三棱柱的表面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
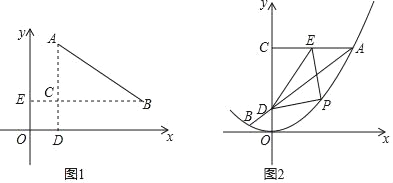
【题目】(1)如图1,若点A坐标为(x1,y1),点B坐标为(x2,y2),作AD⊥x轴于点D,BE⊥y轴于点E,AD与BE相交于点C,则有AC=|y1﹣y2|,BC=|x1﹣x2|,所以,A、B两点间的距离为AB=![]() .
.
根据结论,若M、N两点坐标分别为(1,4)、(5,1),则MN= (直接写出结果).
(2)如图2,直线y=kx+1与y轴相交于点D,与抛物线y=![]() x2相交于A,B两点,A点坐标为(4,a),过点A作y轴的垂线交y轴于点C,E是AC中点,点P是第一象限内直线AB下方抛物线上一动点,连接PE、PD、ED;
x2相交于A,B两点,A点坐标为(4,a),过点A作y轴的垂线交y轴于点C,E是AC中点,点P是第一象限内直线AB下方抛物线上一动点,连接PE、PD、ED;
①a= ,k= ,AD= (直接写出结果).
②若△DEP是以DE为底的等腰三角形,求点P的横坐标;
③求四边形CDPE的周长的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
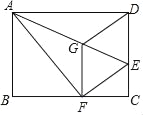
【题目】如图,将矩形ABCD沿AE折叠,点D的对应点落在BC上点F处,过点F作FG∥CD,连接EF,DG,下列结论中正确的有( )
①∠ADG=∠AFG;②四边形DEFG是菱形;③DG2=![]() AEEG;④若AB=4,AD=5,则CE=1.
AEEG;④若AB=4,AD=5,则CE=1.
A. ①②③④ B. ①②③ C. ①③④ D. ①②
查看答案和解析>>
科目:初中数学 来源: 题型:
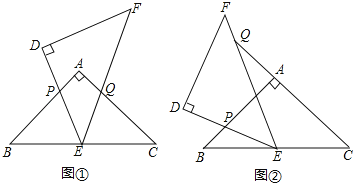
【题目】如图,![]() 和
和![]() 是两个全等的等腰直角三角形,
是两个全等的等腰直角三角形,![]() ,
,![]() 的顶点E与
的顶点E与![]() 的斜边BC的中点重合
的斜边BC的中点重合![]() 将
将![]() 绕点E旋转,旋转过程中,线段DE与线段AB相交于点P,线段EF与射线CA相交于点Q.
绕点E旋转,旋转过程中,线段DE与线段AB相交于点P,线段EF与射线CA相交于点Q.
![]() 如图
如图![]() ,当点Q在线段AC上,且
,当点Q在线段AC上,且![]() 时,
时,![]() 和
和![]() 的形状有什么关系,请证明;
的形状有什么关系,请证明;
![]() 如图
如图![]() ,当点Q在线段CA的延长线上时,
,当点Q在线段CA的延长线上时,![]() 和
和![]() 有什么关系,说明理由;
有什么关系,说明理由;
![]() 当
当![]() ,
,![]() 时,求P、Q两点间的距离.
时,求P、Q两点间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
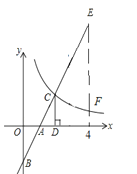
【题目】如图,在直角坐标系中,直线y1=2x﹣2与坐标轴交于A,B两点,与双曲线y2=![]() (x>0)交于点C,过点C作CD⊥x轴,垂足为D,且OA=AD,则以下结论:①当x>0时,y1随x的增大而增大,y2随x的增大而减小;②
(x>0)交于点C,过点C作CD⊥x轴,垂足为D,且OA=AD,则以下结论:①当x>0时,y1随x的增大而增大,y2随x的增大而减小;②![]() ;③当0<x<2时,y1<y2;④如图,当x=4时,EF=4.其中正确结论的个数是( )
;③当0<x<2时,y1<y2;④如图,当x=4时,EF=4.其中正确结论的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】仔细阅读下面例题,解答问题:
例题,已知二次三项式x2-4x+m有一个因式是(x+3),求另一个因式以及m的值.
解:设另一个因式为(x+n),得x2-4x+m=(x+3)(x+n),
则x2-4x+m=x2+(n+3)x+3n.
∴![]() ,
,
解得n=-7,m=-21,
∴另一个因式为(x-7),m的值为-21.
问题:仿照以上方法解答下面问题:
已知二次三项式3x2+5x-m有一个因式是(3x-1),求另一个因式以及m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
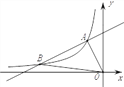
【题目】如图,一次函数y=k1x+b的图象与反比例函数y=![]() (x<0)的图象相交于点A(-1,2)、点B(-4,n).
(x<0)的图象相交于点A(-1,2)、点B(-4,n).
(1)求此一次函数和反比例函数的表达式;
(2)求△AOB的面积;
(3)在x轴上存在一点P,使△PAB的周长最小,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com