
【题目】如图,![]() 和
和![]() 是两个全等的等腰直角三角形,
是两个全等的等腰直角三角形,![]() ,
,![]() 的顶点E与
的顶点E与![]() 的斜边BC的中点重合
的斜边BC的中点重合![]() 将
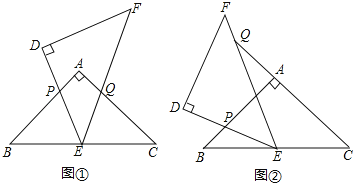
将![]() 绕点E旋转,旋转过程中,线段DE与线段AB相交于点P,线段EF与射线CA相交于点Q.
绕点E旋转,旋转过程中,线段DE与线段AB相交于点P,线段EF与射线CA相交于点Q.
![]() 如图
如图![]() ,当点Q在线段AC上,且
,当点Q在线段AC上,且![]() 时,
时,![]() 和
和![]() 的形状有什么关系,请证明;
的形状有什么关系,请证明;
![]() 如图
如图![]() ,当点Q在线段CA的延长线上时,
,当点Q在线段CA的延长线上时,![]() 和
和![]() 有什么关系,说明理由;
有什么关系,说明理由;
![]() 当
当![]() ,
,![]() 时,求P、Q两点间的距离.
时,求P、Q两点间的距离.
 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
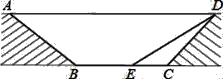
【题目】(10分)一块材料的形状是锐角三角形ABC,边BC=120mm,高AD=80mm,把它加工成正方形零件如图1,使正方形的一边在BC上,其余两个顶点分别在AB、AC上.

(1)求证:△AEF∽△ABC;
(2)求这个正方形零件的边长;
(3)如果把它加工成矩形零件如图2,问这个矩形的最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为缓解交通拥堵,某区拟计划修建一地下通道,该通道一部分的截面如图所示(图中地面AD与通道BC平行,通道水平宽度BC为8米,∠BCD=135°,通道斜面CD的长为6米,通道斜面AB的坡度i=1:![]() .
.
(1)求通道斜面AB的长;
(2)为增加市民行走的舒适度,拟将设计图中的通道斜面CD的坡度变缓,修改后的通道斜面DE的坡角为30°,求此时BE的长.
(答案均精确到0.1米,参考数据:![]() ≈1.41,
≈1.41,![]() ≈2.24,
≈2.24,![]() ≈2.45)
≈2.45)
查看答案和解析>>
科目:初中数学 来源: 题型:
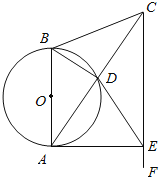
【题目】如图,在△ABC中,AB=CB,以AB为直径的⊙O交AC于点D.过点C作CF∥AB,在CF上取一点E,使DE=CD,连接AE.对于下列结论:①AD=DC;②△CBA∽△CDE;③![]() =
=![]() ;④AE为⊙O的切线,一定正确的结论全部包含其中的选项是( )
;④AE为⊙O的切线,一定正确的结论全部包含其中的选项是( )
A. ①② B. ①②③ C. ①④ D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图①,在ABCD中,O为对角线BD的中点.过O的直线MN交直线AB于点M,交直线CD于点N;过O的另一条直线PQ交直线AD于点P,交直线BC于点Q,连接PN、MQ.
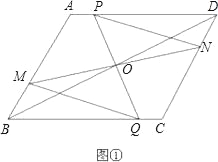

(1)试证明△PON与△QOM全等;
(2)若点O为直线BD上任意一点,其他条件不变,则△PON与△QOM又有怎样的关系?试就点O在图②所示的位置,画出图形,证明你的猜想;
(3)若点O为直线BD上任意一点(不与点B、D重合),设OD:OB=k,PN=x,MQ=y,则y与x之间的函数关系式为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作出反比例函数y=-![]() 的图象,并结合图象回答:(1)当x=2时,y的值;(2)当1<x≤4时,y的取值范围;(3)当1≤y<4时,x的取值范围.
的图象,并结合图象回答:(1)当x=2时,y的值;(2)当1<x≤4时,y的取值范围;(3)当1≤y<4时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的切线,A为切点,AC是⊙O的弦,过O作OH⊥AC于点H.若OH=3,AB=8,BO=10.求:
(1)⊙O的半径;
(2)弦AC的长(结果保留根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
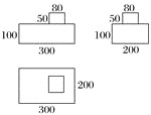
【题目】已知一个模型的三视图如图,其边长如图所示(单位:cm).制作这个模型的木料密度为150 kg/m3,则这个模型的质量是多少kg?如果油漆这个模型,每千克油漆可以漆4 m2,需要油漆多少kg?(质量=密度×体积)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com