Question

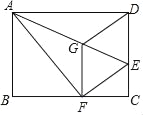
【题目】如图，将矩形ABCD沿AE折叠，点D的对应点落在BC上点F处，过点F作FG∥CD，连接EF，DG，下列结论中正确的有（　　）

①∠ADG=∠AFG；②四边形DEFG是菱形；③DG2=AEEG；④若AB=4，AD=5，则CE=1．

A. ①②③④ B. ①②③ C. ①③④ D. ①②

Answer 1

【答案】B

【解析】（1）由折叠的性质可得：∠ADG=∠AFG（故①正确）；

（2）由折叠的性质可知：∠DGE=∠FGE，∠DEG=∠FEG，DE=FE，

∵FG∥CD，

∴∠FGE=∠DEG，

∴∠DGE=∠FEG，

∴DG∥FE，

∴四边形DEFG是平行四边形，

又∵DE=FE，

∴四边形DEFG是菱形（故②正确）；

（3）如图所示，连接DF交AE于O，

∵四边形DEFG为菱形，

∴GE⊥DF，OG=OE=GE，

∵∠DOE=∠ADE=90°，∠OED=∠DEA，

∴△DOE∽△ADE，

∴，即DE2=EOAE，

∵EO=GE，DE=DG，

∴DG2=AEEG，故③正确；

（4）由折叠的性质可知，AF=AD=5，DE=FE，

∵AB=4，∠B=90°，

∴BF=，

∴FC=BC-BF=2，

设CE=x，则FE=DE=4-x，

在Rt△CEF中，由勾股定理可得： ，解得： .

故④错误；

综上所述，正确的结论是①②③.

故选B.