
【题目】如图,在平行四边形![]() 中,
中,![]() ,
,![]() 是
是![]() 中点,
中点,![]() 在
在![]() 延长线上,连接
延长线上,连接![]() 相交于点
相交于点![]() .
.

(1)若![]() ,求平行四边形
,求平行四边形![]() 的面积;
的面积;
(2)若![]() ,求证:
,求证:![]() .
.
【答案】(1)18;(2)见解析
【解析】
(1)过点A作AH⊥BC于H,由AC=BC,∠ABC=75°,得出∠ACB=30°,则AH=![]() AC=
AC=![]() BC=3,S平行四边形ABCD=2S△ABC=2×
BC=3,S平行四边形ABCD=2S△ABC=2×![]() BCAH,即可得出结果;
BCAH,即可得出结果;
(2)过点A作AN∥CE,交BG于N,则∠ECA=∠CAN,由E是AB中点得出EF是△ABN的中位线,则EF=![]() AN,证明∠GBC=∠ECA,∠GBC=∠G,∠ACB=∠CAG得出∠ECB=∠ECA=∠CAN=∠GAN,推出∠GAN=∠G,则AN=GN,由平行线的性质得出
AN,证明∠GBC=∠ECA,∠GBC=∠G,∠ACB=∠CAG得出∠ECB=∠ECA=∠CAN=∠GAN,推出∠GAN=∠G,则AN=GN,由平行线的性质得出![]() =
=![]() =1,得出BF=FN,即可得出结论.
=1,得出BF=FN,即可得出结论.
(1)解:作![]() ,垂足为
,垂足为![]() ,则
,则![]()
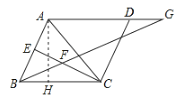
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
(2)过点A作AN∥CE,交BG于N,如图2所示:
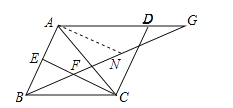
则∠ECA=∠CAN,
∵E是AB中点,
∴EF是△ABN的中位线,
∴EF=![]() AN,
AN,
∵AC=BC,E是AB中点,
∴∠ECB=∠ECA,
∵∠GBC=∠ECB,
∴∠GBC=∠ECA,
∵四边形ABCD是平行四边形,
∴BC∥AD,
∴∠GBC=∠G,∠ACB=∠CAG,
∴∠ECB=∠ECA=∠CAN=∠GAN,
∴∠GAN=∠G,
∴AN=GN,
∵EF∥AN,
![]() ,
,
∴BF=FN
∴GF=GN+FN=AN+BF,
∴GF=BF+2EF.


 优百分课时互动系列答案
优百分课时互动系列答案科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 经过原点O及点A
经过原点O及点A![]() 和点B
和点B![]() .
.
(1)求抛物线的解析式;
(2)如图1,设抛物线的对称轴与x轴交于点C,将直线![]() 沿y轴向下平移n个单位后得到直线l,若直线l经过B点,与y轴交于点D,且与抛物线的对称轴交于点E.若P是抛物线上一点,且PB=PE,求点P的坐标;
沿y轴向下平移n个单位后得到直线l,若直线l经过B点,与y轴交于点D,且与抛物线的对称轴交于点E.若P是抛物线上一点,且PB=PE,求点P的坐标;
(3)如图2,将抛物线向上平移9个单位得到新抛物线,直接写出下列两个问题的答案:
①直线![]() 至少向上平移多少个单位才能与新抛物线有交点?
至少向上平移多少个单位才能与新抛物线有交点?
②新抛物线上的动点Q到直线![]() 的最短距离是多少?
的最短距离是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
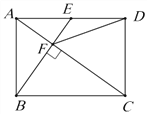
【题目】如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为F,连接DF,下列四个结论:①△AEF∽△CAB ;②![]() ;③DF=DC; ④CF=2AF.
;③DF=DC; ④CF=2AF.
其中正确的结论是________________(填番号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一拱桥的截面呈抛物线形状,抛物线两端点与水面的距离都是1m,拱桥的跨度为10m,拱桥与水面的最大距离是5m,桥洞两侧壁上各有一盏距离水面4m景观灯.
(1)求抛物线的解析式;
(2)求两盏景观灯之间的水平距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆警车沿着一条南北方向的公路巡视,某天早晨从![]() 地出发,晚上到达
地出发,晚上到达![]() 地,约定向北为正方向,当天行驶记录如下(单位:千米):
地,约定向北为正方向,当天行驶记录如下(单位:千米):![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
(1)问![]() 地在
地在![]() 地的哪个方向?相距多少千米?
地的哪个方向?相距多少千米?
(2)若警车出发时邮箱里剩油18升,该警车每小时耗油0.2升,请问警车在到达B地之前是否需要加油?若需要,至少加多少升油?
查看答案和解析>>
科目:初中数学 来源: 题型:
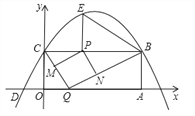
【题目】如图,矩形OABC的两边在坐标轴上,点A的坐标为(10,0),抛物线y=ax2+bx+4过点B,C两点,且与x轴的一个交点为D(﹣2,0),点P是线段CB上的动点,设CP=t(0<t<10).
(1)请直接写出B、C两点的坐标及抛物线的解析式;
(2)过点P作PE⊥BC,交抛物线于点E,连接BE,当t为何值时,∠PBE=∠OCD?
(3)点Q是x轴上的动点,过点P作PM∥BQ,交CQ于点M,作PN∥CQ,交BQ于点N,当四边形PMQN为正方形时,请求出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
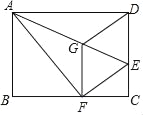
【题目】如图,将矩形ABCD沿AE折叠,点D的对应点落在BC上点F处,过点F作FG∥CD,连接EF,DG,下列结论中正确的有( )
①∠ADG=∠AFG;②四边形DEFG是菱形;③DG2=![]() AEEG;④若AB=4,AD=5,则CE=1.
AEEG;④若AB=4,AD=5,则CE=1.
A. ①②③④ B. ①②③ C. ①③④ D. ①②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据阅读材料,解决问题.
数n是一个三位数,各数位上的数字互不相同,且都不为零,从它各数位上的数字中任选两个构成一个两位数,这样就可以得到六个不同的两位数,我们把这六个不同的两位数叫做数n的“生成数”.数n的所有“生成数”之和与22的商记为G(n),例如n=123,它的六个“生成数”是12,13,21,23,31,32,这六个“生成数”的和12+13+21+23+31+32=132,132÷22=6,所以G(123)=6.
(1)计算:G(125),G(746);
(2)数s,t是两个三位数,它们都有“生成数”,a,1,4分别是s的百位、十位、个位上的数字,x,y,6分别是t的百位、十位、个位上的数字,规定:k=![]() ,若G(s)G(t)=84,求k的最小值.
,若G(s)G(t)=84,求k的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
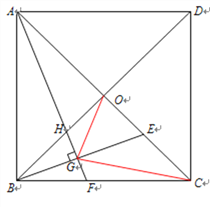
【题目】如图,在正方形ABCD中,对角线AC、BD相交于点O,E为OC上动点(与点O不重合),作AF⊥BE,垂足为G,交BC于F,交B0于H,连接OG,CC.
(1)求证:AH=BE;
(2)试探究:∠AGO的度数是否为定值?请说明理由;
(3)若OG⊥CG,BG=![]() ,求△OGC的面积.
,求△OGC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com