
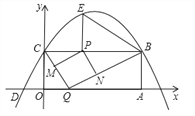
ЁОЬтФПЁПШчЭМЃЌОиаЮOABCЕФСНБпдкзјБъжсЩЯЃЌЕуAЕФзјБъЮЊЃЈ10ЃЌ0ЃЉЃЌХзЮяЯпy=ax2+bx+4Й§ЕуBЃЌCСНЕуЃЌЧвгыxжсЕФвЛИіНЛЕуЮЊDЃЈЉ2ЃЌ0ЃЉЃЌЕуPЪЧЯпЖЮCBЩЯЕФЖЏЕуЃЌЩшCP=tЃЈ0ЃМtЃМ10ЃЉЃЎ
ЃЈ1ЃЉЧыжБНгаДГіBЁЂCСНЕуЕФзјБъМАХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЙ§ЕуPзїPEЁЭBCЃЌНЛХзЮяЯпгкЕуEЃЌСЌНгBEЃЌЕБtЮЊКЮжЕЪБЃЌЁЯPBE=ЁЯOCDЃП
ЃЈ3ЃЉЕуQЪЧxжсЩЯЕФЖЏЕуЃЌЙ§ЕуPзїPMЁЮBQЃЌНЛCQгкЕуMЃЌзїPNЁЮCQЃЌНЛBQгкЕуNЃЌЕБЫФБпаЮPMQNЮЊе§ЗНаЮЪБЃЌЧыЧѓГіtЕФжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉBЃЈ10ЃЌ4ЃЉЃЌCЃЈ0ЃЌ4ЃЉЃЌ![]() ЃЛЃЈ2ЃЉ3ЃЛЃЈ3ЃЉ
ЃЛЃЈ2ЃЉ3ЃЛЃЈ3ЃЉ![]() Лђ
Лђ ![]() .
.
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉгЩХзЮяЯпЕФНтЮіЪНПЩЧѓЕУCЕузјБъЃЌгЩОиаЮЕФаджЪПЩЧѓЕУBЕузјБъЃЌгЩBЁЂDЕФзјБъЃЌРћгУД§ЖЈЯЕЪ§ЗЈПЩЧѓЕУХзЮяЯпНтЮіЪНЃЛ
ЃЈ2ЃЉПЩЩшPЃЈtЃЌ4ЃЉЃЌдђПЩБэЪОГіEЕузјБъЃЌДгЖјПЩБэЪОГіPBЁЂPEЕФГЄЃЌгЩЬѕМўПЩжЄЕУЁїPBEЁзЁїOCDЃЌРћгУЯрЫЦШ§НЧаЮЕФаджЪПЩЕУЕНЙигкtЕФЗНГЬЃЌПЩЧѓЕУtЕФжЕЃЛ
ЃЈ3ЃЉЕБЫФБпаЮPMQNЮЊе§ЗНаЮЪБЃЌдђПЩжЄЕУЁїCOQЁзЁїQABЃЌРћгУЯрЫЦШ§НЧаЮЕФаджЪПЩЧѓЕУCQЕФГЄЃЌдкRtЁїBCQжаПЩЧѓЕУBQЁЂCQЃЌдђПЩгУtЗжБ№БэЪОГіPMКЭPNЃЌПЩЕУЕНЙигкtЕФЗНГЬЃЌПЩЧѓЕУtЕФжЕЃЎ
ЪдЬтНтЮіЃК
НтЃКЃЈ1ЃЉдкyЃНax2ЃЋbxЃЋ4жаЃЌСюxЃН0ПЩЕУyЃН4ЃЌ
ЁрCЃЈ0ЃЌ4ЃЉЃЌ
ЁпЫФБпаЮOABCЮЊОиаЮЃЌЧвAЃЈ10ЃЌ0ЃЉЃЌ
ЁрBЃЈ10ЃЌ4ЃЉЃЌ
АбBЁЂDзјБъДњШыХзЮяЯпНтЮіЪНПЩЕУ![]() ЃЌ
ЃЌ
НтЕУ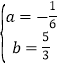 ЃЌ
ЃЌ
ЁрХзЮяЯпНтЮіЪНЮЊyЃН![]() x2ЃЋ
x2ЃЋ![]() xЃЋ4ЃЛ
xЃЋ4ЃЛ
ЃЈ2ЃЉгЩЬтвтПЩЩшPЃЈtЃЌ4ЃЉЃЌдђEЃЈtЃЌ![]() t2ЃЋ
t2ЃЋ![]() tЃЋ4ЃЉЃЌ
tЃЋ4ЃЉЃЌ
ЁрPBЃН10ЉtЃЌPEЃН![]() t2ЃЋ
t2ЃЋ![]() tЃЋ4Љ4ЃН
tЃЋ4Љ4ЃН![]() t2ЃЋ
t2ЃЋ![]() tЃЌ
tЃЌ
ЁпЁЯBPEЃНЁЯCODЃН90ЁуЃЌ
ЕБЁЯPBEЃНЁЯOCDЪБЃЌ
дђЁїPBEЁзЁїOCDЃЌ
Ёр![]() ЃЌМДBPODЃНCOPEЃЌ
ЃЌМДBPODЃНCOPEЃЌ
Ёр2ЃЈ10ЉtЃЉЃН4ЃЈ![]() t2ЃЋ
t2ЃЋ![]() tЃЉЃЌНтЕУtЃН3ЛђtЃН10ЃЈВЛКЯЬтвтЃЌЩсШЅЃЉЃЌ
tЃЉЃЌНтЕУtЃН3ЛђtЃН10ЃЈВЛКЯЬтвтЃЌЩсШЅЃЉЃЌ
ЁрЕБtЃН3ЪБЃЌЁЯPBEЃНЁЯOCDЃЛ
ЕБЁЯPBEЃНЁЯCDOЪБЃЌ
дђЁїPBE/span>ЁзЁїODCЃЌ
Ёр![]() ЃЌМДBPOCЃНDOPEЃЌ
ЃЌМДBPOCЃНDOPEЃЌ
Ёр4ЃЈ10ЉtЃЉЃН2ЃЈ![]() t2ЃЋ
t2ЃЋ![]() tЃЉЃЌНтЕУtЃН12ЛђtЃН10ЃЈОљВЛКЯЬтвтЃЌЩсШЅЃЉ
tЃЉЃЌНтЕУtЃН12ЛђtЃН10ЃЈОљВЛКЯЬтвтЃЌЩсШЅЃЉ
злЩЯЫљЪіЁрЕБtЃН3ЪБЃЌЁЯPBEЃНЁЯOCDЃЛ
ЃЈ3ЃЉЕБЫФБпаЮPMQNЮЊе§ЗНаЮЪБЃЌдђЁЯPMCЃНЁЯPNBЃНЁЯCQBЃН90ЁуЃЌPMЃНPNЃЌ
ЁрЁЯCQOЃЋЁЯAQBЃН90ЁуЃЌ
ЁпЁЯCQOЃЋЁЯOCQЃН90ЁуЃЌ
ЁрЁЯOCQЃНЁЯAQBЃЌ
ЁрRtЁїCOQЁзRtЁїQABЃЌ
Ёр![]() ЃЌМДOQAQЃНCOABЃЌ
ЃЌМДOQAQЃНCOABЃЌ
ЩшOQЃНmЃЌдђAQЃН10ЉmЃЌ
ЁрmЃЈ10ЉmЃЉЃН4ЁС4ЃЌНтЕУmЃН2ЛђmЃН8ЃЌ
ЂйЕБmЃН2ЪБЃЌCQЃН![]() ЃН
ЃН![]() ЃЌBQЃН
ЃЌBQЃН![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁрsinЁЯBCQЃН![]() ЃН
ЃН![]() ЃЌsinЁЯCBQЃН
ЃЌsinЁЯCBQЃН![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁрPMЃНPCsinЁЯPCQЃН![]() tЃЌPNЃНPBsinЁЯCBQЃН
tЃЌPNЃНPBsinЁЯCBQЃН![]() ЃЈ10ЉtЃЉЃЌ
ЃЈ10ЉtЃЉЃЌ
Ёр![]() t ЃН
t ЃН![]() ЃЈ10ЉtЃЉЃЌНтЕУtЃН
ЃЈ10ЉtЃЉЃЌНтЕУtЃН![]() ЃЌ
ЃЌ
ЂкЕБmЃН8ЪБЃЌЭЌРэПЩЧѓЕУtЃН![]() ЃЌ
ЃЌ
ЁрЕБЫФБпаЮPMQNЮЊе§ЗНаЮЪБЃЌtЕФжЕЮЊ![]() Лђ
Лђ![]() ЃЎ
ЃЎ


 ЛЦИдЙкОќПЮПЮСЗЯЕСаД№АИ
ЛЦИдЙкОќПЮПЮСЗЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкОиаЮ![]() жаЃЌ
жаЃЌ![]() бизХЖдНЧЯп
бизХЖдНЧЯп![]() ЗелФмгы
ЗелФмгы![]() жиКЯЃЌЧв
жиКЯЃЌЧв![]() гы
гы![]() НЛгкЕу
НЛгкЕу![]() ЃЌШє
ЃЌШє![]() ЃЌдђ
ЃЌдђ![]() ЕФУцЛ§ЮЊ__________.
ЕФУцЛ§ЮЊ__________.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПКЏЪ§y=![]() ЪЧЗДБШР§КЏЪ§ЃЎ
ЪЧЗДБШР§КЏЪ§ЃЎ
ЃЈ1ЃЉЧѓmЕФжЕЃЛ
ЃЈ2ЃЉжИГіИУКЏЪ§ЭМЯѓЫљдкЕФЯѓЯоЃЌдкУПИіЯѓЯоФкЃЌyЫцxЕФдіДѓШчКЮБфЛЏЃП
ЃЈ3ЃЉХаЖЯЕуЃЈ![]() ЃЌ2ЃЉЪЧЗёдкетИіКЏЪ§ЕФЭМЯѓЩЯЃЎ
ЃЌ2ЃЉЪЧЗёдкетИіКЏЪ§ЕФЭМЯѓЩЯЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
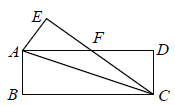
ЁОЬтФПЁПШчЭМЃЌСтаЮABCDжаЃЌЕуMЁЂNЗжБ№дкADЃЌBCЩЯЃЌЧвAMЃНCNЃЌMNгыACНЛгкЕуOЃЌСЌНгDOЃЌШєЁЯBACЃН28ЁуЃЌдђЁЯODCЃН_____ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНааЫФБпаЮ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЪЧ
ЪЧ![]() жаЕуЃЌ
жаЕуЃЌ![]() дк
дк![]() бгГЄЯпЩЯЃЌСЌНг
бгГЄЯпЩЯЃЌСЌНг![]() ЯрНЛгкЕу
ЯрНЛгкЕу![]() .
.

ЃЈ1ЃЉШє![]() ЃЌЧѓЦНааЫФБпаЮ
ЃЌЧѓЦНааЫФБпаЮ![]() ЕФУцЛ§ЃЛ
ЕФУцЛ§ЃЛ
ЃЈ2ЃЉШє![]() ЃЌЧѓжЄЃК
ЃЌЧѓжЄЃК![]() .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЬНЫїЙцТЩЃЌЙлВьЯТУцЫуЪНЃЌНтД№ЮЪЬтЃЎ
1ЃЋ3ЃН4ЃН22ЃЛ
1ЃЋ3ЃЋ5ЃН9ЃН32ЃЛ
1ЃЋ3ЃЋ5ЃЋ7ЃН16ЃН42ЃЛ
1ЃЋ3ЃЋ5ЃЋ7ЃЋ9ЃН25ЃН52ЃЛ
Ё
(1)ЧыВТЯыЃК1ЃЋ3ЃЋ5ЃЋ7ЃЋ9ЃЋЁЃЋ19ЃН________ЃЛ
(2)ЧыВТЯыЃК1ЃЋ3ЃЋ5ЃЋ7ЃЋ9ЃЋЁЃЋ(2nЃ1)ЃН________ЃЛ
(3)ЪдМЦЫуЃК101ЃЋ103ЃЋЁЃЋ197ЃЋ199.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫЬсИпбЇЩњЪщаДККзжЕФФмСІЃЌдіЧПБЃЛЄККзжЕФвтЪЖЃЌЮвЪаОйАьСЫЪзНьЁАККзжЬ§аДДѓШќЁБЃЌОбЁАЮКѓга50УћбЇЩњВЮМгОіШќЃЌет50УћбЇЩњЭЌЪБЬ§аД50ИіККзжЃЌШєУПе§ШЗЬ§аДГівЛИіККзжЕУ1ЗжЃЌИљОнВтЪдГЩМЈЛцжЦГіВПЗжЦЕЪ§ЗжВМБэКЭВПЗжЦЕЪ§ЗжВМжБЗНЭМШчЭМБэЃК
зщБ№ | ГЩМЈxЗж | ЦЕЪ§ЃЈШЫЪ§ЃЉ |
Ек1зщ | 25ЁмxЃМ30 | 6 |
Ек2зщ | 30ЁмxЃМ35 | 8 |
Ек3зщ | 35ЁмxЃМ40 | 16 |
Ек4зщ | 40ЁмxЃМ45 | a |
Ек5зщ | 45ЁмxЃМ50 | 10 |

ЧыНсКЯЭМБэЭъГЩЯТСаИїЬтЃК
ЃЈ1ЃЉЧѓБэжаaЕФжЕЃЛЃЈ2ЃЉЧыАбЦЕЪ§ЗжВМжБЗНЭМВЙГфЭъећЃЛ
ЃЈ3ЃЉЕк5зщ10УћЭЌбЇжаЃЌга4УћФаЭЌбЇЃЌЯжНЋет10УћЭЌбЇЦНОљЗжГЩСНзщНјааЖдПЙСЗЯАЃЌЧв4УћФаЭЌбЇУПзщЗжСНШЫЃЌЧѓаЁгюгыаЁЧПСНУћФаЭЌбЇФмЗждкЭЌвЛзщЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
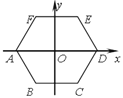
ЁОЬтФПЁПШчЭМЃЌе§СљБпаЮ ABCDEFЕФжааФгызјБъдЕуOжиКЯЃЌЦфжаA(-2ЃЌ0)ЃЎНЋСљБпаЮ ABCDEFШЦдЕуOАДЫГЪБеыЗНЯђа§зЊ2018ДЮЃЌУПДЮа§зЊ60ЁуЃЌдђа§зЊКѓЕуAЕФЖдгІЕуA'ЕФзјБъЪЧЃЈ ЃЉЃЎ
A. (1ЃЌ![]() ) B. (
) B. (![]() ЃЌ1) C. (1ЃЌ
ЃЌ1) C. (1ЃЌ![]() ) D. (-1ЃЌ
) D. (-1ЃЌ![]() )
)
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЩЬГЁгћЙКНјЙћжвћСЯКЭЬМЫсвћСЯЙВ60ЯфЃЌСНжжвћСЯУПЯфЕФНјМлКЭЪлМлШчЯТБэЫљЪОЁЃЩшЙКНјЙћжвћСЯxЯфЃЈxЮЊе§ећЪ§ЃЉЃЌЧвЫљЙКНјЕФСНжжвћСЯФмШЋВПТєГіЃЌЛёЕУЕФзмРћШѓЮЊWдЊЃЈзЂЃКзмРћШѓЃНзмЪлМлЃзмНјМлЃЉЁЃ
ЃЈ1ЃЉЩшЩЬГЁЙКНјЬМЫсвћСЯyЯфЃЌжБНгаДГіyгыxЕФКЏЪ§НтЮіЪНЃЛ
ЃЈ2ЃЉЧѓзмРћШѓwЙигкxЕФКЏЪ§НтЮіЪНЃЛ
ЃЈ3ЃЉШчЙћЙКНјСНжжвћСЯЕФзмЗбгУВЛГЌЙ§2100дЊЃЌФЧУДИУЩЬГЁШчКЮНјЛѕВХФмЛёРћзюЖрЃПВЂЧѓГізюДѓРћШѓЁЃ
вћСЯ | ЙћжвћСЯ | ЬМЫсвћСЯ |
НјМлЃЈдЊ/ЯфЃЉ | 40 | 25 |
ЪлМлЃЈдЊ/ЯфЃЉ | 52 | 32 |
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com