
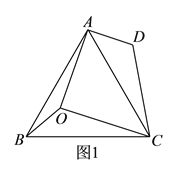
【题目】已知,点![]() 是等边
是等边![]() 内的任一点,连接
内的任一点,连接![]() ,
,![]() ,
,![]() .
.
如图![]() ,已知
,已知![]() ,
,![]() ,将
,将![]() 绕点
绕点![]() 按顺时针方向旋转
按顺时针方向旋转![]() ,使
,使![]() 与
与![]() 重合,得
重合,得![]() .
.
(![]() )
)![]() 的度数是__________.
的度数是__________.
(![]() )用等式表示线段
)用等式表示线段![]() ,
,![]() ,
,![]() 之间的数量关系,并证明.(图
之间的数量关系,并证明.(图![]() 为备用图)
为备用图)
【答案】(![]() )
)![]() ;(
;(![]() )
)![]() ,证明见解析.
,证明见解析.
【解析】试题分析:
(1)由已知条件易得∠AOC=360°-150°-120°=90°,由旋转的性质易得:∠ADC=∠BOC=120°,∠DCO=60°,结合四边形的内角和为360°即可得到∠DAO=360°-90°-60°-120°=90°;
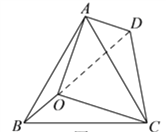
(2)如图3,将△BOC绕点C按顺时针方向旋转60°得到△ADC,连接OD,由旋转的性质可知AD=BO,CD=CO,∠OCD=60°,由此可得△OCD是等边三角形,从而可得OC=OD,结合(1)中结论∠DAO=90°由勾股定理即可得到:OB2+OA2=OC2.
试题解析:
(1)∵△ADC是由△BOC绕点C顺时针旋转60°得到的,
∴∠ADC=∠BOC=120°,∠DCO=60°,
又∵∠AOC=360°-∠AOB-∠BOC=360°-150°-120°=90°,
∴在四边形AOCD中,∠DAO=360°-120°-60°-90°=90°;
(![]() )
)![]() .理由如下:
.理由如下:
如图3,将△BOC绕点C按顺时针方向旋转60°得到△ADC,连接OD,由旋转的性质可知AD=BO,CD=CO,∠OCD=60°,
∴△OCD是等边三角形,
∴OC=OD,
由(1)可知∠DAO=90°,
∴在Rt△DAO中,![]() ,
,
∴OA2+OB2=OC2.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图所示为一机器零件的三视图.
(1)请写出符合这个机器零件形状的几何体的名称.
(2)若俯视图中三角形为正三角形,那么请根据图中所标的尺寸,计算这个几何体的表面积(单位:cm2).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在研究相似问题时,甲、乙同学的观点如下:
甲:将边长为3、4、5的三角形按图1的方式向外扩张,得到新三角形,它们的对应边间距为1,则新三角形与原三角形相似.
乙:将邻边为3和5的矩形按图2的方式向外扩张,得到新的矩形,它们的对应边间距均为1,则新矩形与原矩形不相似.
对于两人的观点,下列说法正确的是( )

A. 两人都对 B. 两人都不对 C. 甲对,乙不对 D. 甲不对,乙对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=![]() ,△ACD沿AD折叠,使得点C落在斜边AB上的点E处.
,△ACD沿AD折叠,使得点C落在斜边AB上的点E处.
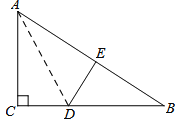
(1)问:△BDE与△BAC相似吗?
(2)已知AC=6,BC=8,求线段AD的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
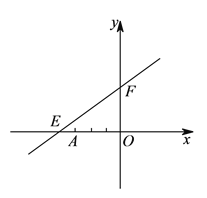
【题目】如图,直线![]() 与
与![]() 轴
轴![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
(![]() )求
)求![]() 的值.
的值.
(![]() )若点
)若点![]() 是第二象限内的直线
是第二象限内的直线![]() 上的一个动点,在点
上的一个动点,在点![]() 的运动过程中,试写出
的运动过程中,试写出![]() 的面积
的面积![]() 与
与![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个半径为18 cm的圆,从中心挖去一个正方形,当挖去的正方形的边长由小变大时,剩下部分的面积也随之发生变化.
(1)若挖去的正方形边长为x(cm),剩下部分的面积为y(cm2),则y与x之间的关系式是什么?
(2)当挖去的正方形的边长由1 cm变化到9 cm时,剩下部分的面积由____变化到____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列解题过程:已知![]() 、
、![]() 、
、![]() 为△ABC的三边,且满足
为△ABC的三边,且满足![]() ,
,
试判断△ABC的形状.
解:∵![]() ①
①
∴![]() ②
②
∴![]() ③
③
∴△ABC为直角三角形.
问:(1)上述解题过程,从哪一步开始出现错误?请写出该步的代号________;
(2)错误的原因是____________________________;
(3)本题的正确结论是_________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在边长为a的正方形中挖去一个边长为b的小正方形(a>b)(如图甲),把余下的部分拼成一个矩形(如图乙),根据两个图形中阴影部分的面积相等,可以验证( )

A. (a+b)2=a2+2ab+b2
B. (a﹣b)2=a2﹣2ab+b2
C. a2﹣b2=(a+b)(a﹣b)
D. (a+2b)(a﹣b)=a2+ab﹣2b2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小军同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).
(1)请根据题中已有的信息补全频数分布表和频数分布直方图;
月均用水量/t | 频数 | 百分比 |
2≤x<3 | 2 | 4% |
3≤x<4 | 12 | 24% |
4≤x<5 | ||
5≤x<6 | 10 | 20% |
6≤x<7 | 12% | |
7≤x<8 | 3 | 6% |
8≤x<9 | 2 | 4% |
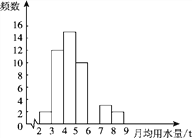
(2)如果家庭月均用水量“大于或等于4 t且小于7 t”为中等用水量家庭,请你通过样本估计总体中的中等用水量家庭大约有多少户.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com