
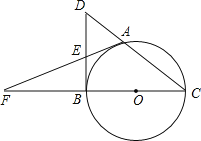
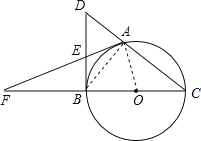
【题目】如图,A是以BC为直径的⊙O上一点,过点B作⊙O的切线,与CA的延长线相交于点D,E是BD的中点,延长AE与CB的延长线相交于点F.
(1)求证:AF是⊙O的切线;
(2)若BE=5,BF=12,求CD的长.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)利用直角三角形斜边中线的性质和等边对等角得到∠EAB=∠EBA,结合⊙O的切线得出OA⊥AF,从而得出AF是⊙O的切线;
(2)先根据勾股定理求得EF的长,再根据切线的性质得出EB=EA=5,即可求得AF的长,然后根据切割线定理求得FC,进而得出BC的长,根据E是BD的中点,得出BD的长,最后根据勾股定理即可求得CD的长.
解:(1)连接AB,OA,
∵BC是⊙O的直径,
∴∠BAC=90°,
∵DB是⊙O的切线,
∴DB⊥BC,
∴∠DBO=90°,
在RT△ABD中,E是斜边BD的中线,
∴AE=DE=BE,
∴∠EAB=∠EBA,
∵OA=OB,
∴∠OAB=∠OBA,
∴∠EAB+∠OAB=∠EBA+∠OBA
∴∠EAO=∠DBO=90°,
∴OA⊥AF,
∴AF是⊙O的切线;
(2)∵在RT△BEF中,BE=5,BF=12,
∴EF=![]() =13,
=13,
∵FA、DB是⊙O的切线,
∴EA=EB=5,
∴AF=EF+EA=13+5=18,
∵AF2=FBFC,
∴FC=![]()
∴BC=FC﹣FB=27﹣12=15,
∵E是BD的中点,
∴BD=2BE=10,
在RT△DBC中,![]() .
.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
【题目】郑州市创建国家生态园林城市实施方案已经出台,到2019年5月底,市区主城区要达到或超过《国家生态园林城市标准》各项指标要求.郑州市林荫路推广率要超过85%,在推进此活动中,郑州市某小区决定购买A、B两种乔木树,经过调查,获取信息如下:如果购买A种树木40棵,B种树木60棵,需付款11400元;如果购买A种树木50棵,B种树木50棵,需付款10500元.
树种 | 购买数量低于50棵 | 购买数量不低于50棵 |
A | 原价销售 | 以八折销售 |
B | 原价销售 | 以九折销售 |
(1)A种树木与B种树木的单价各多少元?
(2)经过测算,需要购置A、B两种树木共100棵,其中B种树木的数量不多于A种树木的三分之一,如何购买付款最少?最少费用是多少元?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
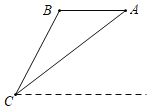
【题目】如图,无人飞机从A点水平飞行10秒至B点,在地面上C处测得A点、B点的仰角分别为45°,75°,已知无人飞机的飞行速度为80米/秒,则这架无人飞机的飞行高度为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
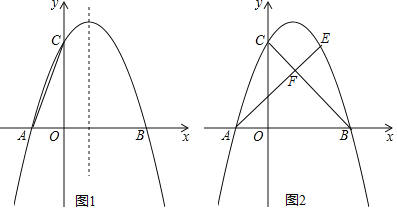
【题目】如图,抛物线y=ax2+bx+4与x轴交于点A(﹣1,0)、B(3,0),与y轴交于点C.
(1)求抛物线的解析式;
(2)如图1,D为抛物线对称轴上一动点,求D运动到什么位置时△DAC的周长最小;
(3)如图2,点E在第一象限抛物线上,AE与BC交于点F,若AF:FE=2:1,求E点坐标;
(4)点M、N同时从B点出发,分别沿BA、BC方向运动,它们的运动速度都是1个单位/秒,当点M运动到点A时,点N停止运动,则当点N停止运动后,在x轴上是否存在点P,使得△PBN是等腰三角形?若存在,直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小轩从如图所示的二次函数y=ax2+bx+c(a≠0)的图象中,观察得出了下面五条信息:
①ab>0;②a+b+c<0;③b+2c>0;④a﹣2b+4c>0;⑤![]() .
.
你认为其中正确信息的个数有
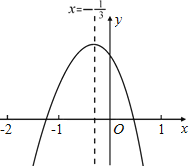
A.2个 B.3个 C.4个 D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
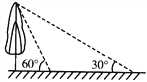
【题目】如图,校园内有一棵与地面垂直的树,数学兴趣小组两次测量它在地面上的影子,第一次是阳光与地面成60°角时,第二次是阳光与地面成30°角时,两次测量的影长相差8米,则树高_____________米(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
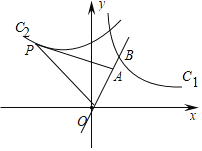
【题目】如图,将曲线c1:y=![]() (x>0)绕原点O逆时针旋转60°得到曲线c2,A为直线y=
(x>0)绕原点O逆时针旋转60°得到曲线c2,A为直线y=![]() x上一点,P为曲线c2上一点,PA=PO,且△PAO的面积为6
x上一点,P为曲线c2上一点,PA=PO,且△PAO的面积为6![]() ,直线y=
,直线y=![]() x交曲线c1于点B,则OB的长( )
x交曲线c1于点B,则OB的长( )
A.2![]() B.5C.3
B.5C.3![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
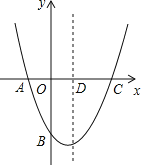
【题目】如图,在平面直角坐标系中,二次函数y=ax2+bx-![]() 的图象经过点A(-1,0)、C(2,0),与y轴交于点B,其对称轴与x轴交于点D
的图象经过点A(-1,0)、C(2,0),与y轴交于点B,其对称轴与x轴交于点D
(1)求二次函数的表达式及其顶点坐标;
(2)M(s,t)为抛物线对称轴上的一个动点,
①若平面内存在点N,使得A、B、M、N为顶点的四边形为矩形,直接写出点M的坐标;
②连接MA、MB,若∠AMB不小于60°,求t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com