
【题目】某学校九年级举行乒乓球比赛,准备发放一些奖品进行奖励,奖品设为一等奖和二等奖.已知购买一个一等奖奖品比购买一个二等奖奖品多用20元.若用400元购买一等奖奖品的个数是用160元购买二等奖奖品个数的一半.
(1)求购买一个一等奖奖品和一个二等奖奖品各需多少元?
(2)经商谈,商店决定给予该学校购买一个一等奖奖品即赠送一个二等奖奖品的优惠,如果该学校需要二等奖奖品的个数是一等奖奖品个数的2倍还多8个,且该学校购买两个奖项奖品的总费用不超过670元,那么该学校最多可购买多少个一等奖奖品?
【答案】(1)购买一个二等奖奖品需5元,购买一个一等奖奖品需25元.
(2)该学校最多可购买21个一等奖奖品.
【解析】
(1)设购买一个二等奖奖品需x元,则购买一个一等奖奖品需(x+20)元,根据数量=总价÷单价结合用400元购买一等奖奖品的个数是用160元购买二等奖奖品个数的一半,即可得出关于x的分式方程,解之经检验后即可得出结论;
(2)设该学校可购买a个一等奖奖品,则可购买(2a+8)个二等奖奖品,根据总价=单价×购买数量结合该学校购买两个奖项奖品的总费用不超过670元,即可得出关于a的一元一次不等式,解之取其中的最大值即可得出结论.
(1)设购买一个二等奖奖品需x元,则购买一个一等奖奖品需(x+20)元,
根据题意得:![]() =
=![]() ,
,
解得:x=5,
经检验,x=5是原分式方程的解,
∴x+20=25.
答:购买一个二等奖奖品需5元,购买一个一等奖奖品需25元.
(2)设该学校可购买a个一等奖奖品,则可购买(2a+8)个二等奖奖品,
根据题意得:15a+5(2a+8a)670,
解得:a21.
答:该学校最多可购买21个一等奖奖品.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源: 题型:
【题目】嫦娥四号探测器于2019年1月3日,成功着陆在月球背面,通过“鹊桥”中继星传回了世界第一张近距离拍摄的月背影像图,开启了人类月球探测新篇章.当中继星成功运行于地月拉格朗日L2点时,它距离地球约1500000km.用科学记数法表示数1500000为( )

A. 15×105 B. 1.5×106 C. 0.15×107 D. 1.5×105
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题提出】
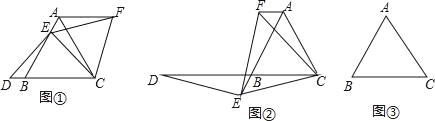
如图①,已知△ABC是等腰三角形,点E在线段AB上,点D在直线BC上,且ED=EC,将△BCE绕点C顺时针旋转60°至△ACF连接EF
试证明:AB=DB+AF
【类比探究】
(1)如图②,如果点E在线段AB的延长线上,其他条件不变,线段AB,DB,AF之间又有怎样的数量关系?请说明理由
(2)如果点E在线段BA的延长线上,其他条件不变,请在图③的基础上将图形补充完整,并写出AB,DB,AF之间的数量关系,不必说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】东东在研究数学问题时遇到一个定义:将三个已经排好顺序数:x1,x2,x3,称为数列x1,x2,x3.计算|x1|,![]() ,
,![]() ,将这三个数的最小值称为数列x1,x2,x3的最佳值.例如,对于数列2,-1,3,因为|2|=2,
,将这三个数的最小值称为数列x1,x2,x3的最佳值.例如,对于数列2,-1,3,因为|2|=2,![]() =
=![]() ,
,![]() =
=![]() ,所以数列2,-1,3的最佳值为
,所以数列2,-1,3的最佳值为![]() .
.
东东进一步发现:当改变这三个数的顺序时,所得到的数列都可以按照上述方法计算其相应的最佳值.如数列-1,2,3的最佳值为![]() ;数列3,-1,2的最佳值为1;….经过研究,东东发现,对于“2,-1,3”这三个数,按照不同的排列顺序得到的不同数列中,最佳值的最小值为
;数列3,-1,2的最佳值为1;….经过研究,东东发现,对于“2,-1,3”这三个数,按照不同的排列顺序得到的不同数列中,最佳值的最小值为![]() .根据以上材料,回答下列问题:
.根据以上材料,回答下列问题:
(1)数列-4,-3,1的最佳值为
(2)将“-4,-3,2”这三个数按照不同的顺序排列,可得到若干个数列,这些数列的最佳值的最小值为 ,取得最佳值最小值的数列为 (写出一个即可);
(3)将2,-9,a(a>1)这三个数按照不同的顺序排列,可得到若干个数列.若这些数列的最佳值为1,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
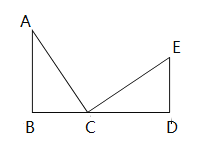
【题目】如图,在△ABC中,∠B=90°,点B、C、D在同一直线上,△ABC≌△CDE,且∠B=∠D,∠BAC=∠DCE.
(1)试说明BD=AB+ED;
(2)若∠CED=2∠BAC,求∠CED的度数;
(3)连接AE,则△ACE是怎样的三角形?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)用“*”表示一种新运算:对于任意正实数a,b,都有![]() .例如,
.例如,![]() ,那么15*27=__;(2)定义一种运算*,其规则为:当a≥b时,a*b=b3;当a<b时,a*b=b2.根据这个规则,方程3*x=27的解是__.
,那么15*27=__;(2)定义一种运算*,其规则为:当a≥b时,a*b=b3;当a<b时,a*b=b2.根据这个规则,方程3*x=27的解是__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为提供节约用水,某市按如下规定每月收取水费,若一户居民每月用水不超过20立方米,则每立方米按3元收费;若超过20立方米,前20立方米收费标准不变,超过部分每立方米按5元收费,若某户居民某月用水![]() 立方米.
立方米.
(1)试用含![]() (
(![]() >20)的代数式表示这户居民该月应缴的水费.
>20)的代数式表示这户居民该月应缴的水费.
(2)已知该市小李家1月份用水13立方米,2月份用水22立方米,3月份用水17立方米,求他家这三个月应缴纳水费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把几个不同的数用大括号围起来,中间用逗号断开,如:{3,4},{-3,6,8,18},我们称之为集合,其中大括号内的数称其为集合的元素,如果一个集合满足:只要其中有一个元素a,使得-2a+4也是这个集合的元素,这样的集合我们称为条件集合,例如:集合{3,2},因为-2×3+4=-2,-2恰好是这个集合的元素,所以{3,-2}是条件集合:例如:集合{-2,9,8},因为-2×(-2)+4=8,8恰好是这个集合的元素,所以{-2,9,8}是条件集合.
(1)集合{-4,12}______条件集合;集合{![]() ,-
,-![]() ,
,![]() }______条件集合 (填“是”或“不是”)
}______条件集合 (填“是”或“不是”)
(2)若集合{8,10,n}是条件集合,求n的所有可能值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com