
【题目】如图,一次函数y=x+k图象过点A(1,0),交y轴于点B,C为y轴负半轴上一点,且OB=![]() BC,过A,C两点的抛物线交直线AB于点D,且CD∥x轴.
BC,过A,C两点的抛物线交直线AB于点D,且CD∥x轴.
(1)求这条抛物线的解析式;
(2)直接写出使一次函数值小于二次函数值时x的取值范围.

【答案】(1)y=x2+2x﹣3;(2)x<﹣2或x>1
【解析】试题(1)利用待定系数法求解即可得;
(2)结合图象即可进行判断出x的取值范围.
试题解析:(1)把A(1,0)代入y=x+k中,得k=﹣1,
∴y=x﹣1,令x=0,得点B坐标为(0,﹣1),

∵OB=![]() BC,OB=1,∴BC=2,∴OC=3,
BC,OB=1,∴BC=2,∴OC=3,
∴C点坐标为(0,﹣3),
又CD∥x轴,
∴点D的纵坐标为﹣3代入y=x﹣1得x=﹣2,
∴点D的坐标为(﹣2,﹣3),
设抛物线解析式为y=ax2+bx+c,
将A(1,0),C(0,﹣3),D(﹣2,﹣3)代入,得
 ,解得
,解得 ,
,
∴抛物线的解析式为:y=x2+2x﹣3;
(2)∵直线与抛物线交于D(﹣2,﹣3),A(1,0)两点,抛物线开口向上,
∴当x<﹣2或x>1时,一次函数值小于二次函数值.


 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:
【题目】某公司计划十月份组织员工到外地旅游,人数在10~30人之间.甲、乙两个旅行社的服务质量相同,且价格都是每人500元.甲旅行社表示可先免去两位游客的旅游费用,其余人九折优惠,乙旅行社表示给予每位游客八折优惠.
(1)写出甲乙两个旅行社收费y与人数x之间的函数关系式.
(2)如果你是这次出游的组织者,当去多少人时两家旅行社的总费用相同.
(3)当去17人时,选哪家旅行社更优惠?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AE=CF,∠A=∠C,那么添加下列一个条件后,仍无法判定△ADF≌△CBE的是( )
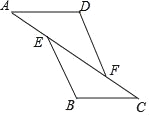
A. ∠D=∠B B. AD=CB C. BE=DF D. ∠AFD=∠CEB
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC中,AD⊥BC于点D,BD=2,以AD为一边向右作等边三角形ADE.

(1)求△ABC的周长;
(2)判断AC、DE的位置关系,并给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点O在对角线AC上,以OA的长为半径的⊙O与AD,AC分别交于点E,F,且∠ACB=∠DCE,tan∠ACB=![]() ,BC=2cm.以下结论:
,BC=2cm.以下结论:
①CD=![]() cm; ②AE=DE; ③CE是⊙O的切线; ④⊙O的面积等于
cm; ②AE=DE; ③CE是⊙O的切线; ④⊙O的面积等于![]() cm2.其中正确的结论有_____.(填序号)
cm2.其中正确的结论有_____.(填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠ABC=Rt∠.已知∠A=α,外角∠DCE=β,BC=a,CD=b,则下列结论错误的是( )
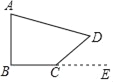
A. ∠ADC=90°﹣α+β B. 点D到BE的距离为bsinβ
C. AD=![]() D. 点D到AB的距离为a+bcosβ
D. 点D到AB的距离为a+bcosβ
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,∠A是锐角,E为边AD上一点,△ABE沿着BE折叠,使点A的对应点F恰好落在边CD上,连接EF,BF.
(1)若∠A=70°,请直接写出∠ABF的度数.
(2)若点F是CD的中点,
①求sinA的值;
②求证:S△ABE=![]() SABCD.
SABCD.
(3)设![]() =k,
=k,![]() =m,试用含k的代数式表示m.
=m,试用含k的代数式表示m.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一张长方形卡片ABCD放在每格宽度为12mm的横格纸中,恰好四个顶点都在横格线上.已知α=36°,求长方形卡片的周长.
(精确到1mm,参考数据:sin36°≈0.60,cos36°≈0.80,tan36°≈0.75)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com