
【题目】如图,在矩形ABCD中,点O在对角线AC上,以OA的长为半径的⊙O与AD,AC分别交于点E,F,且∠ACB=∠DCE,tan∠ACB=![]() ,BC=2cm.以下结论:
,BC=2cm.以下结论:
①CD=![]() cm; ②AE=DE; ③CE是⊙O的切线; ④⊙O的面积等于
cm; ②AE=DE; ③CE是⊙O的切线; ④⊙O的面积等于![]() cm2.其中正确的结论有_____.(填序号)
cm2.其中正确的结论有_____.(填序号)

【答案】①②③.
【解析】
根据正切的定义可以求出AB,由矩形的性质得到CD长,判断①;根据正切的定义求出DE和AE,判断②;根据切线的判定定理判断③;求出⊙O的半径,求出面积,判断④.
∵tan∠ACB=![]() ,
,
∴![]() =
=![]() ,又BC=2cm,
,又BC=2cm,
解得AB=![]() cm,即CD=
cm,即CD=![]() cm,①正确;
cm,①正确;
∵∠ACB=∠DCE,tan∠ACB=![]() ,
,
∴tan∠DCE=![]() ,即
,即![]() =
=![]() ,
,
解得,DE=1,
∵BC=2,
∴AE=1,
∴AE=DE,②正确;
∵四边形ABCD是矩形,
∴BC∥AD,∠ACB=∠DAC;
又∵∠ACB=∠DCE,
∴∠DAC=∠DCE;
连接OE,则∠DAC=∠AEO=∠DCE;
∵∠DCE+∠DEC=90°,
∴∠AE0+∠DEC=90°,
∴∠OEC=90°,即OE⊥CE,
又OE是⊙O的半径,
∴直线CE与⊙O相切,③正确;
在Rt△ADC中,AC=![]() ,
,
在Rt△CEO中,CE2+OE2=OC2,即(![]() )2+12+OE2=(
)2+12+OE2=(![]() ﹣OE)2,
﹣OE)2,
解得,OE=![]() ,
,
④⊙O的面积=π×(![]() )2=
)2=![]() π,④错误,
π,④错误,
故答案为:①②③.


科目:初中数学 来源: 题型:
【题目】游泳是一项深受青少年喜爱的体育活动,学校为了加强学生的安全意识,组织学生观看了纪实片“孩子,请不要私自下水”,并于观看后在本校的2000名学生中作了抽样调查.请根据下面两个不完整的统计图回答以下问题:
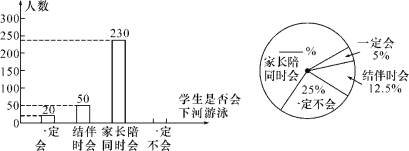
(1)这次抽样调查中,共调查了__ __名学生;
(2)补全两个统计图;
(3)根据抽样调查的结果,估算该校2000名学生中大约有多少人“一定会下河游泳”?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(0<2a<b)的顶点为P(x0,y0),点A(1,yA),B(0,yB),C(﹣1,yC)在该抛物线上,当y0≥0恒成立时,![]() 的最小值为( )
的最小值为( )
A. 1 B. 2 C. 4 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=x+k图象过点A(1,0),交y轴于点B,C为y轴负半轴上一点,且OB=![]() BC,过A,C两点的抛物线交直线AB于点D,且CD∥x轴.
BC,过A,C两点的抛物线交直线AB于点D,且CD∥x轴.
(1)求这条抛物线的解析式;
(2)直接写出使一次函数值小于二次函数值时x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,有一条线段AB,已知点A(﹣3,0)和B(0,4),平移线段AB得到线段A1B1.若点A的对应点A1的坐标为(0,﹣1),则线段AB平移经过的区域(四边形ABB1A1)的面积为( )
A. 12 B. 15 C. 24 D. 30
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】边长为a的正方形ABCD中,点E是BD上一点,过点E作EF⊥AE交射线CB于点F,连结CE.
(1)若点F在边BC上(如图);
①求证:CE=EF;
②若BC=2BF,求DE的长.
(2)若点F在CB延长线上,BC=2BF,请直接写出DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017浙江省嘉兴市,第20题,8分)如图,一次函数![]() (
(![]() )与反比例函数
)与反比例函数![]() (
(![]() )的图象交于点A(﹣1,2),B(m,﹣1).
)的图象交于点A(﹣1,2),B(m,﹣1).
(1)求这两个函数的表达式;
(2)在x轴上是否存在点P(n,0)(n>0),使△ABP为等腰三角形?若存在,求n的值;若不存在,说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com