
【题目】已知抛物线y=ax2+bx+c(0<2a<b)的顶点为P(x0,y0),点A(1,yA),B(0,yB),C(﹣1,yC)在该抛物线上,当y0≥0恒成立时,![]() 的最小值为( )
的最小值为( )
A. 1 B. 2 C. 4 D. 3
【答案】D
【解析】
主要是要是通过相似三角形边的对应关系,构造所求的式子,并对结果找到限制条件即可
 由0<2a<b,得x0=﹣
由0<2a<b,得x0=﹣![]() <﹣1,
<﹣1,
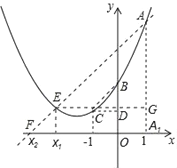
由题意,如图,过点A作AA1⊥x轴于点A1,
则AA1=yA,OA1=1,
连接BC,过点C作CD⊥y轴于点D,则BD=yB﹣yC,CD=1,
过点A作AF∥BC,交抛物线于点E(x1,yE),交x轴于点F(x2,0),
则∠FAA1=∠CBD,
于是Rt△AFA1∽Rt△BCD,
所以![]() =
=![]() ,即
,即![]() =
=![]() ,
,
过点E作EG⊥AA1于点G,
易得△AEG∽△BCD.
有![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∵点A(1,yA)、B(0,yB)、C(﹣1,yC)、E(x1,yE)在抛物线y=ax2+bx+c上,
得yA=a+b+c,yB=c,yC=a﹣b+c,yE=ax12+bx1+c,
∴![]() =
=![]() =1﹣x1,
=1﹣x1,
化简,得x12+x1﹣2=0,解得x1=﹣2(x1=1舍去),
∵y0≥0恒成立,根据题意,有x2≤x1<﹣1,
则1﹣x2≥1﹣x1,即1﹣x2≥3,
∴![]() ≥3,
≥3,
∴![]() 的最小值为3.
的最小值为3.
故选D.


科目:初中数学 来源: 题型:
【题目】已知一张三角形纸片![]() 如图甲
如图甲![]() ,其中
,其中![]() 将纸片沿过点B的直线折叠,使点C落到AB边上的E点处,折痕为
将纸片沿过点B的直线折叠,使点C落到AB边上的E点处,折痕为![]() 如图乙
如图乙![]() 再将纸片沿过点E的直线折叠,点A恰好与点D重合,折痕为
再将纸片沿过点E的直线折叠,点A恰好与点D重合,折痕为![]() 如图丙
如图丙![]() 原三角形纸片ABC中,
原三角形纸片ABC中,![]() 的大小为______
的大小为______![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠BAC=90°,AB=AC,D、E是BC边上的点,将△ABD绕点A旋转,得到△ACD′.

(1)求∠DAD′的度数。
(2)当∠DAE=45°时,求证:DE=D′E;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AE=CF,∠A=∠C,那么添加下列一个条件后,仍无法判定△ADF≌△CBE的是( )
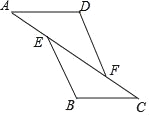
A. ∠D=∠B B. AD=CB C. BE=DF D. ∠AFD=∠CEB
查看答案和解析>>
科目:初中数学 来源: 题型:
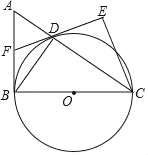
【题目】如图,已知直角△ABC中,∠ABC=90°,BC为圆O的直径,D为圆O与斜边AC的交点,DE为圆O的切线,DE交AB于F,且CE⊥DE.
(1)求证:CA平分∠ECB;
(2)若DE=3,CE=4,求AB的长;
(3)记△BCD的面积为S1,△CDE的面积为S2,若S1:S2=3:2.求sin∠AFD的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC中,AD⊥BC于点D,BD=2,以AD为一边向右作等边三角形ADE.

(1)求△ABC的周长;
(2)判断AC、DE的位置关系,并给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点O在对角线AC上,以OA的长为半径的⊙O与AD,AC分别交于点E,F,且∠ACB=∠DCE,tan∠ACB=![]() ,BC=2cm.以下结论:
,BC=2cm.以下结论:
①CD=![]() cm; ②AE=DE; ③CE是⊙O的切线; ④⊙O的面积等于
cm; ②AE=DE; ③CE是⊙O的切线; ④⊙O的面积等于![]() cm2.其中正确的结论有_____.(填序号)
cm2.其中正确的结论有_____.(填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠ABC=Rt∠.已知∠A=α,外角∠DCE=β,BC=a,CD=b,则下列结论错误的是( )
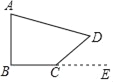
A. ∠ADC=90°﹣α+β B. 点D到BE的距离为bsinβ
C. AD=![]() D. 点D到AB的距离为a+bcosβ
D. 点D到AB的距离为a+bcosβ
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,a、b、c分别是∠A、∠B、∠C的对边,下列条件不能判断△ABC是直角三角形的是( )
A.∠A:∠B:∠C=3:4:5B.a:b:c=7:24:25
C.a2=b2﹣c2D.∠A=∠C﹣∠B
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com